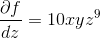Partial Differentiation
Help Questions
Multivariable Calculus › Partial Differentiation
Determine the length of the curve 

Explanation
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Determine the length of the curve 

Explanation
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Find 
Explanation
In order to find 




Natural Log:
Exponential Functions:
Power Functions:
Determine the length of the curve 

Explanation
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral
Determine the length of the curve 

Explanation
First we need to find the tangent vector, and find its magnitude.
Now we can set up our arc length integral