Venn Diagrams

Help Questions

ISEE Upper Level Quantitative Reasoning › Venn Diagrams

Questions 1 - 10

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region. Which of the following is equal to $\overline{A\cup B}$ ?

$\overline{A\cup B} = \left \{ c\right \}$

$\overline{A\cup B} = \left \{ a,c,f\right \}$

$\overline{A\cup B} = \left \{ a,f\right \}$

$\overline{A\cup B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ b,d,e,g,h\right \}$

Explanation

$\overline{A\cup B}$ is the complement of $A\cup B$ - the set of all elements in not in $A\cup B$ .

$A\cup B$ is the union of sets and - the set of all elements in either or . Therefore, $\overline{A\cup B}$ is the set of all elements in neither nor , which can be seen from the diagram to be only one element - . Therefore,

$\overline{A\cup B} = \left \{ c\right \}$

Venn

$\overline{A\cup B} = \left \{ c\right \}$

$\overline{A\cup B} = \left \{ a,c,f\right \}$

$\overline{A\cup B} = \left \{ a,f\right \}$

$\overline{A\cup B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cup B} = \left \{ b,d,e,g,h\right \}$

Explanation

$\overline{A\cup B}$ is the complement of $A\cup B$ - the set of all elements in not in $A\cup B$ .

$\overline{A\cup B} = \left \{ c\right \}$

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region.

What is $A \cap B$ ?

$A \cap B = \left \{ a,f \right \}$

$A \cap B = \left \{ a,b,d,e,f,g,h \right \}$

$A \cap B = \left \{ b,d,e,g,h \right \}$

$A \cap B = \left \{ b,c,d,e,g,h \right \}$

$A \cap B = \left \{ a,c,f \right \}$

Explanation

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . We want all of the letters that fall in both circles, which from the diagram can be seen to be and . Therefore,

$A \cap B = \left \{ a,f \right \}$

Venn

In the above Venn diagram, the universal set is defined as $U = \left \{ a, b, c, d, e, f, g, h\right \}$ . Each of the eight letters is placed in its correct region.

What is $A \cap B$ ?

$A \cap B = \left \{ a,f \right \}$

$A \cap B = \left \{ a,b,d,e,f,g,h \right \}$

$A \cap B = \left \{ b,d,e,g,h \right \}$

$A \cap B = \left \{ b,c,d,e,g,h \right \}$

$A \cap B = \left \{ a,c,f \right \}$

Explanation

$A \cap B = \left \{ a,f \right \}$

The following Venn diagram depicts the number of students who play hockey, football, and baseball. How many students play football and baseball?

Problem_9

Explanation

The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

The following Venn diagram depicts the number of students who play hockey, football, and baseball. How many students play football and baseball?

Problem_9

Explanation

The number of students who play football or baseball can by finding the summer of the number of students who play football alone, baseball alone, baseball and football, and all three sports.

Venn

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ c\right \}$

$\overline{A\cap B} = \left \{ a,c,f\right \}$

$\overline{A\cap B} = \left \{ a,f\right \}$

Explanation

$\overline{A \cap B}$ is the complement of $A \cap B$ - the set of all elements in not in $A \cap B$ .

$A \cap B$ is the intersection of sets and - that is, the set of all elements of that are elements of both and . Therefore, $\overline{A \cap B}$ is the set of all elements that are not in both and , which can be seen from the diagram to be all elements except and . Therefore,

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$ .

Venn

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ b,d,e,g,h\right \}$

$\overline{A\cap B} = \left \{ c\right \}$

$\overline{A\cap B} = \left \{ a,c,f\right \}$

$\overline{A\cap B} = \left \{ a,f\right \}$

Explanation

$\overline{A \cap B}$ is the complement of $A \cap B$ - the set of all elements in not in $A \cap B$ .

$\overline{A\cap B} = \left \{ b,c,d,e,g,h\right \}$ .

A class of students was asked whether they have cats, dogs, or both.The results are depicted in the following Venn diagram. How many students do not have a dog?

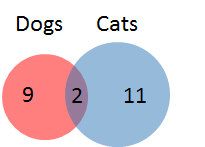
Question_5

Explanation

First, calculate the number of students with a dog:

Next, subtract the number of students with a dog from the total number of students.

A class of students was asked whether they have cats, dogs, or both.The results are depicted in the following Venn diagram. How many students do not have a dog?

Question_5

Explanation

First, calculate the number of students with a dog:

Next, subtract the number of students with a dog from the total number of students.

Page 1 of 2

Return to subject

AI TutorYour personal study buddy

Question of the DayDaily practice to build your skills

FlashcardsStudy and memorize key concepts

WorksheetsBuild custom practice quizzes

AI SolverStep-by-step problem solutions

Learn by ConceptMaster concepts step by step

Diagnostic TestsAssess your knowledge level

Practice TestsTest your skills with exam questions

GamesLearn through free games