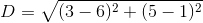How to find length of a line
Help Questions
ISEE Middle Level Quantitative Reasoning › How to find length of a line
What is the length of a line with endpoints 

Explanation
To find the length of this line, you can subtract 

What is the length of a line segment with end points 

Explanation
The length of a line segment can be determined using the distance formula:
Find the slope of a line that passes through 

The slope is undefined.
Explanation
Use the slope formula to solve:
Given the following points.
The slope can be calculated as follows.
Because the 
If you stand on a giant number line at point 

Explanation
The distance on a number line is the number of whole number places between two numbers. When you are going from a negative value to a positive one or vice versa, you must find the distance from 








A right triangle has one leg with a length of 

Explanation
The Pythagorean Theorem states that
Where 


The point 
Explanation
Because the radius is the distance from center to any point on a circle, the distance formula is used to find the measurement of the radius.
A ladder is leaning on a wall. It is 

Explanation
The Pythagorean Theorem states that:
With 


If a circle has a radius of 
Explanation
The diameter of the circle would be the longest line that can be drawn within that circle.
Because radius is half of the diameter, the diameter is calculated by multiplying the radius of the circle by two.
If the radius is 

The coordinates of 


Explanation
A rectangle has two diagonals with the same length. Therefore, use the distance formula to calculate the distance.
Line 




Explanation
First, write each portion of the statement in mathematical terms.
Since AB=80 we will substitute that into the equation.
Now that we know AC we can calculate AD as follows.