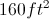How to find the length of the side of a trapezoid
Help Questions
Geometry › How to find the length of the side of a trapezoid
An isosceles trapezoid has base measurements of 


Explanation
To solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths. Since this problem provides the length for both of the bases as well as the total perimeter, the missing sides can be found using the following formula: Perimeter= Base one 


Thus, the solution is:
Check the solution by plugging in the answer:
Find the value of 


Explanation
The formula to find the area of a trapezoid is

Substitute in the values for the area, a base, and the height. Then solve for 
An isosceles trapezoid has base measurements of 


Explanation
In order to solve this problem, first note that an isosceles trapezoid has two parallel bases that are nonequivalent in length. Additionally, an isosceles trapezoid must have two nonparallel sides that have equivalent lengths.
This problem provides the lengths for each of the bases as well as the height of the isosceles trapezoid. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid, first use the height of the trapezoid to form right triangles on the interior of the trapezoid that each have a base length of 

Note: the base length of 
Now, apply the formula 

Thus, the solution is:
Find the value of 


Explanation
The formula to find the area of a trapezoid is

Substitute in the values for the area, a base, and the height. Then solve for 
Suppose the area of the trapezoid is 


Explanation
Write the formula for finding the area of a trapezoid.
Substitute the givens and solve for either base.
Find the value of 


Explanation
The formula to find the area of a trapezoid is

Substitute in the values for the area, a base, and the height. Then solve for 
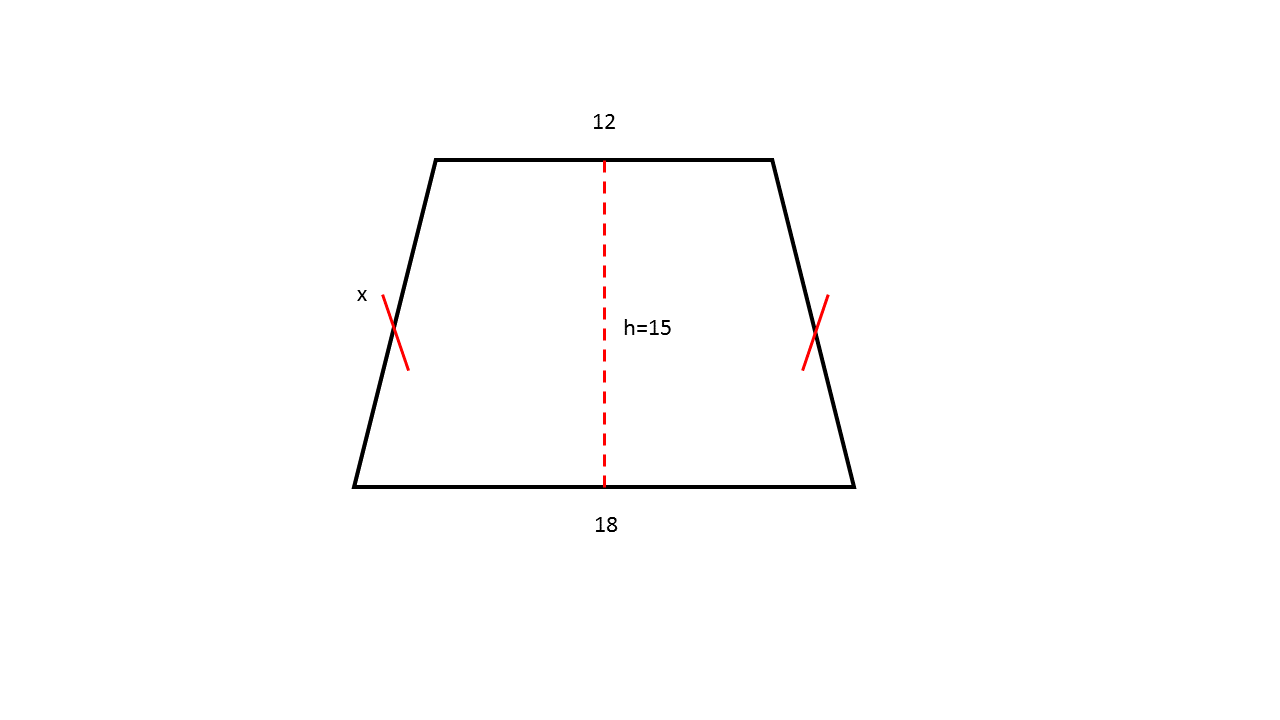
The isosceles trapezoid shown above has base measurements of 



Explanation
In this problem the lengths for each of the bases and the height of the isosceles trapezoid is provided in the question prompt. In order to find the length for one of the two equivalent nonparallel legs of the trapezoid (side 

The base of the interior triangles is equal to 

Now, apply the pythagorean theorem: 

Thus,
Find the area of the following trapezoid.

Explanation
The correct answer is 128 sq ft.
There are two ways to find the total area. One way to find the total area, you must find the area of the triangle and rectangle separately. After some deduction 

To find the area of the triangle, you would multiply 6 by 8 and then divide by 2 to get 24. To find the area of the rectangle, you would multiply 8 by 13 to get 104. Then you would add both areas to get 128 sq ft.

The other way to find the area is to use the formula for area of a trapezoid. After some deduction 
Then you use the formula:
to get
Find the value of 


Explanation
The formula to find the area of a trapezoid is

Substitute in the values for the area, a base, and the height. Then solve for 

Using the trapezoid shown above, find the length of side 
Explanation
In order to find the length of side 





Thus, the solution can be found by applying the formula: