How to find if of acute / obtuse isosceles triangles are congruent
Help Questions
Geometry › How to find if of acute / obtuse isosceles triangles are congruent

Refer to the above diagram. 


The Side-Side-Side Postulate
The Hinge Theorem
The Converse of the Isosceles Triangle Theorem
The Isosceles Triangle Theorem
The Side-Angle-Side Postulate
Explanation
In addition to the fact that 



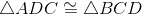
Given: 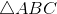

Which statement(s) must be true?
(a)
(b)
Neither (a) nor (b)
(a) but not (b)
(b) but not (a)
(a) and (b)
Explanation
Neither similarity nor congruence of the two triangles follows from the statements given, as can be seen from the figure below:
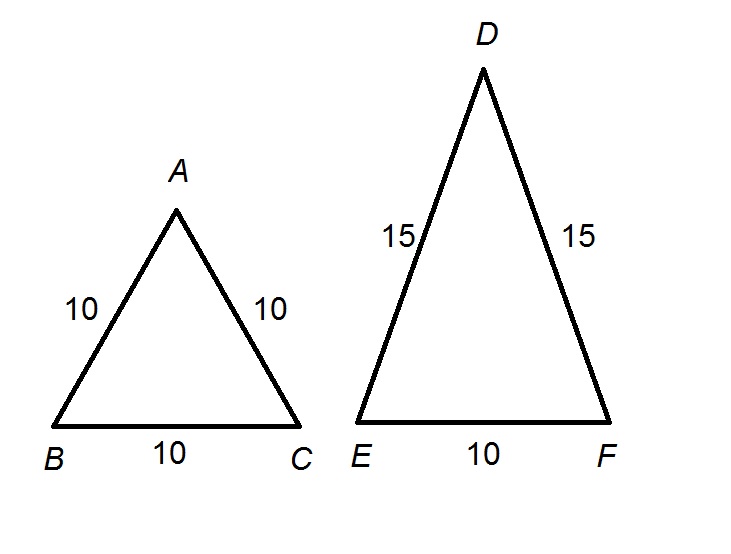

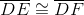

and

The triangles are not similar, and thus cannot be congruent either, so neither statement holds.