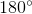All Intermediate Geometry Resources
Example Questions
Example Question #891 : Intermediate Geometry
There is a regular hexagon with a side length of 
cannot be determined
Given that the hexagon is a regular hexagon, this means that all the side length are congruent and all internal angles are congruent. The question requires us to solve for the measure of an internal angle. Given the aforementioned definition of a regular polygon, this means that there must only be one correct answer.
In order to solve for the answer, the question provides additional information that isn't necessarily required. The measure of an internal angle can be solved for using the equation:


In this case, 
For this problem, the information about the side length may be negated.
Example Question #1 : How To Find An Angle In A Hexagon
What is the interior angle of a regular hexagon if the area is 15?
The area has no relevance to find the angle of a regular hexagon.
There are 6 sides in a regular hexagon. Use the following formula to determine the interior angle.
Substitute 
Since there are 6 sides, divide this number by 6 to determine the value of each interior angle.
Example Question #1 : How To Find An Angle In A Hexagon
Given: Regular Hexagon 




True or false: Quadrilateral 
True
False
False
Below is regular Hexagon 



Each angle of a regular hexagon measures 

The angles of a rectangle must measure 

Example Question #91 : Hexagons
True or false: Each of the six angles of a regular hexagon measures 
True
False
True
A regular polygon with 

Setting 
The statement is therefore true.
Example Question #91 : Hexagons
True or false: Each of the exterior angles of a regular hexagon measures 
False
True
False
If one exterior angle is taken at each vertex of any polygon, and their measures are added, the sum is 

Solve for 
The statement is false.
Example Question #6 : How To Find An Angle In A Hexagon
Given: Hexagon 
True, false, or undetermined: Hexagon 
True
False
Undetermined
False
Suppose Hexagon 

A hexagon has 6 sides, so set 
Since one angle is given to be of measure 
Example Question #1 : How To Find An Angle In A Hexagon
What is the measure of one exterior angle of a regular twenty-sided polygon?
The sum of the exterior angles of any polygon, one at each vertex, is 

Example Question #8 : How To Find An Angle In A Hexagon
Which of the following cannot be the six interior angle measures of a hexagon?
All of these can be the six interior angle measures of a hexagon.
All of these can be the six interior angle measures of a hexagon.
The sum of the interior angle measures of a hexagon is
Add the angle measures in each group.
In each case, the angle measures add up to 720, so the answer is that all of these can be the six interior angle measures of a hexagon.
All Intermediate Geometry Resources