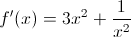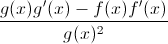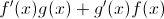All High School Math Resources
Example Questions
Example Question #71 : Derivatives
Find the derivative of the following function:
Since this function is a polynomial, we take the derivative of each term separately.
From the power rule, the derivative of
is simply
We can rewrite 
and using the power rule again, we get a derivative of

So the answer is
Example Question #72 : Derivatives
What is
The chain rule is "first times the derivative of the second plus second times derivative of the first".
In this case, that means 
Example Question #82 : Calculus I — Derivatives
What is the first derivative of 
Since we're adding terms, we take the derivative of each part separately. For 
Remember, 
Example Question #61 : Finding Derivatives
What is the second derivative of 
To find the second derivative, we need to start by finding the first one.
Since we're adding terms, we take the derivative of each part separately. For 
Remember, 
Now we repeat the process, but using 
Example Question #73 : Derivatives
Which of the following best represents 
The question is just asking for the Quotient Rule formula.
Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.
Given,
the bottom function is 



Substituting these into the Quotient Rule formula resulting in the following.
All High School Math Resources