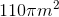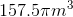All High School Math Resources
Example Questions
Example Question #1 : Other Polyhedrons
Find the surface area of the following half-cylinder.
The formula for the surface area of a half-cylinder must include one-half of the surface area of a cylinder, which would be:
We also need to add the area of the new rectangular face that is created by cutting the cylinder in half. The area of this rectangle would be:
where the length of the rectangle is the same as the height of the half-cylinder, and the width of the rectangle is the same as the diameter of the base of the half-cylinder. So we can rewrite the area of the rectangle as:
Now we can combine the two area formulas to find the total surface area of the half-cylinder:
where 


Plugging in our values, we get:
Example Question #1 : How To Find The Surface Area Of A Polyhedron
Find the surface area of the following polyhedron.

The formula for the surface area of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Example Question #3 : Other Polyhedrons
Find the surface area of the following polyhedron.

The formula for the surface area of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Example Question #2 : How To Find The Surface Area Of A Polyhedron
Find the surface area of the following polyhedron.

The formula for the surface area of a polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Other Polyhedrons
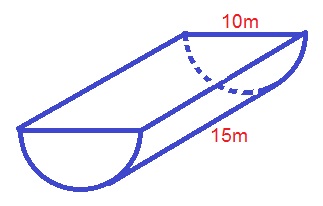
Find the volume of the following half cylinder.

The formula for the volume of a half-cylinder is:
where 

Plugging in our values, we get:
Example Question #6 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
Where 


Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
where 



Use the formula for a 
Plugging in our values, we get:
Example Question #8 : Other Polyhedrons
Find the volume of the following polyhedron.

The formula for the volume of the polyhedron is:
where 

Use the formula for a 
Plugging in our values, we get:
All High School Math Resources