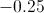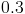All High School Math Resources
Example Questions
Example Question #1 : Calculus I — Derivatives
Consider the function
Find the minimum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90588/gif.latex)
To find potential minima of the function, take the first derivative of 
Set the derivative to 0:
We solve for 

We can double check that 
which means the function is concave up, so that the point we found is a minimum.
Example Question #1 : Calculus I — Derivatives
What is the local maximum of 

There is no local maximum.
To find the maximum, we need to look at the first derivative.
To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.
We're going to treat 

Notice that 
When looking at the first derivative, remember that if the output of this equation is positive, the original function is increasing. If the derivative is negative, then the function is decreasing.
Notice that 

We can find that root using the quadratic equation:
Since we're looking for a negative value, we will subtract.
Therefore, the maximum is at 
Example Question #1 : Identifying Absolute And Local Extrema
What is the local maximum of 


There is no maximum between these two points.
To find the maximum, we must find where the graph shifts from increasing to decreasing. To find out the rate at which the graph shifts from increasing to decreasing, we look at the second derivative and see when the value changes from positive to negative.
That is to say, we will look at the second derivative and see where (if at all) the graph crosses the x-axis and is moving from a positive y-value to a negative y-value.
Now we must find the second derivative. Unfortunately, the derivatives of trig functions must be memorized. The first derivative is:

To find the second derivative, we take the derivative of our result.

Therefore, the second derivative will be 
Does our new equation cross the x-axis and move from positive to negative between 




Example Question #2 : Identifying Absolute And Local Extrema
What is the local minimum of 

To find the local minimum of 
To find the first derivative, we can use the power rule. The power rule states that we multiply each variable by its current exponent and then lower that exponent by one.
Simplify.
Anything to the zero power is one, so 
Therefore, 
At the minimum, our 

From here we split off into two roots, one where we add and one where we subtract:
and
Do both of these roots satisfy 
Then we move on to our next question: Does the graph shift from negative to positive at either of these roots? Yes. When 
Therefore, the local minimum is at 
Example Question #3 : Identifying Absolute And Local Extrema
What is the absolute minimum of 
To find the minimum we need to look at the first derivative.
Since we're adding terms, we take the derivative of each part separately. For 
Remember, 
Now we need to find the roots of the derivative.
Does 


Our next question is, "Does the graph change from negative to positive at that point?" Yes. This means that our parent function has shifted from decreasing to increasing at that point.
Therefore, this will be our minimum.
Example Question #1 : Calculus I — Derivatives
What is the local minimum of 

There is no local minimum.
A local minimum occurs when a graph "bottoms out" -- it has been decreasing, it slows down, stops, and then begins to increase. At that point when it switches from decreasing to increasing, our first derivative should move from negative to positive. Start by finding the first derivative and then see if that happens.
To find the first derivative of 
The power rule states that we multiply each variable by its current exponent and then lower the exponent of each variable by one.
Since 


Anything times zero is zero, so our final term 
Simplify what we have.
Our first derivative, then, is 
Graph the equation 

The zero occurs when 

Example Question #2 : Identifying Absolute And Local Extrema
What is the local minimum of 

The y-value is constant throughout that range.
There is no local minimum in that range.
To find the maximum, we need to look at the first derivative.
To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.
We're going to treat 

Notice that 
When looking at the first derivative, remember that if the output of this equation is positive, the original function is increasing. If the derivative is negative, then the function is decreasing.
Because we want the MINIMUM, we want to see where the derivative changes from negative to positive.
Notice that 


Certified Tutor
Certified Tutor
All High School Math Resources