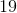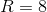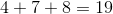Equations
Help Questions
Math › Equations
Questions 1 - 1
1
In Spot’s toy basket he has 

Explanation
To solve this problem, we first have to find our unknowns. Our unknowns are the number of ropes and stuffed animals that Spot has. We can set up equations for these unknowns by letting 






Now we need to add up our number of balls, stuffed animals and ropes to find our total.
AI TutorYour personal study buddy
Questions of the DayDaily practice to build your skills
FlashcardsStudy and memorize key concepts
WorksheetsBuild custom practice quizzes
AI SolverStep-by-step problem solutions
Learn by ConceptMaster concepts step by step
Diagnostic TestsAssess your knowledge level
Practice TestsTest your skills with exam questions
GamesLearn through free games