All GRE Math Resources
Example Questions
Example Question #51 : Quadrilaterals
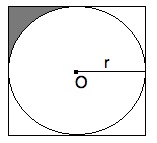
In the figure above, the circle is inscribed within the bounding square. If r = 5, what is the area of the shaded region?
100π
100
100 - 25π
25 - (25/4)π
25π
25 - (25/4)π
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
Example Question #51 : Quadrilaterals
Find the area of a square with a side length of 4.
24
16
8
32
16
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
Example Question #52 : Quadrilaterals
If one doubles the radius of the semi-circle on the right of the diagram above, by what percentage does the overall area of the diagram change?
100%
200%
300%
150%
400%
300%
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
Example Question #53 : Quadrilaterals
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
Example Question #54 : Quadrilaterals
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
It cannot be determined from the information provided.
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 
Example Question #55 : Quadrilaterals

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is 
The area of the square is then 
Example Question #3 : How To Find The Area Of A Square
Square 





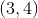
Quantity A: The area of square
Quantity B: 24
The information cannot be determined based on the information provided
Quantity A is greater
Quantity B is greater
The two quantities are equal
Quantity A is greater
If you draw points 

All GRE Math Resources