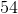All Calculus 1 Resources
Example Questions
Example Question #2 : Calculus Review
Consider the position function 
Find the function which models the velocity of the oxygen molecule.
Recall that velocity is the first derivative of position and acceleration is the second derivative of position.
So given:
Apply the power rule to each term to find the velocity.
Example Question #41 : How To Find Velocity
Consider the position function 
Find the velocity of the oxygen molecule after 
Recall that velocity is the first derivative of position and acceleration is the second derivative of position.
So given:
To find the velocity after 4 seconds, find v(4)
Example Question #42 : How To Find Velocity
The displacement of an object at time 


The velocity is defined as the derivative of the displacement equation. With the displacement equation 
Remember that 
In our case our
Thus, the velocity equation is defined as:


The velocity at 
Example Question #41 : Velocity
The position of an object is given by the equation 
The velocity of the object can be found by differentiating the equation 
We can rewrite the equation as


Thus, the velocity equation is:
Example Question #44 : How To Find Velocity
The position of an object is given by the equation 

The velocity equation can be found by differentiating the equation for position 
This gives the equation
At t=0
Example Question #45 : How To Find Velocity
The acceleration of an object is given by the equation 

The velocity equation can be found by integrating the acceleration equation.
Differentiating the equation 
Using the initial velocity of the equation gives us
The complete equation for the velocity is
Example Question #46 : How To Find Velocity
If the acceleration of an object is 

To find the velocity from the acceleration function, integrate the acceleration function 
We will also need to know the time when the object at 
Substitute this value back into the acceleration function and solve for time.
Substitute this value to the velocity function to find the velocity.
Example Question #42 : Spatial Calculus
If the position function of a ball is 

To find the velocity function, take the derivative of the position function:
Remember when integrating, increase the exponent of each term by one and then divide the term by the value of the new exponent.
Substitute the time into the velocity function.
Example Question #43 : How To Find Velocity
The acceleration of an object is given by the equation 


Using the acceleration equation, 
Now using the initial velocity of 50, we can find
Now we can solve for the velocity at t=10
Example Question #41 : Spatial Calculus
The position equation for an object is 

The velocity of the object can be found by differentiating the position equation. To differentiate this equation, the power rule and the chain rule must be used.
The power rule says that

The chain rule says that

Differentiating the equation 

Using 0 as the value for t gives us

Certified Tutor
All Calculus 1 Resources