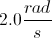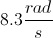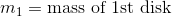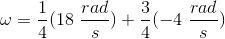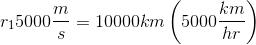All AP Physics C: Mechanics Resources
Example Questions
Example Question #71 : Motion
An ice skater begins to spin, starting with his arms spread out as far as possible, parallel to the ice. He pulls his arms into his body, and then raises them completely vertically towards the ceiling. As the skater pulls his arms inward, his angular velocity will __________, and as he raises his arms vertically his angular velocity will __________.
decrease . . . stay the same
decrease . . . increase
increase . . . stay the same
increase . . . decrease
increase . . . stay the same
Through conservation of angular momentum, as moment of inertia decreases, the angular velocity increases. Moment of inertia is dependent on the distribution of the spinning body's mass away from the center of mass—as the skater brings his arms in, he lowers his moment of inertia, thus increasing his angular velocity. If he raises his arms completely vertically from this point, it does not change the radius of mass distributions (from the center of his body), thus maintaining his angular velocity.
Example Question #72 : Ap Physics C
Sarah spins a ball of mass 




By the conservation of angular momentum, the angular momentum 
Here, 


Substitute.
We are given that 

Example Question #2 : Understanding Conservation Of Angular Momentum

A child is standing at the center of a frictionless, rotating platform. Both the child and the platform are rotating with and initial angular velocity, 
Total momentum
Rotational inertia of the disk
Total rotational kinetic energy
Total angular inertia
Total angular momentum
Total rotational kinetic energy
Since the platform is frictionless, as the child walks, angular momentum is conserved. However, since there is an 

Example Question #72 : Mechanics Exam
Two solid cylinderical disks have equal radii. The first disk is spinning clockwise at 

For the first disk, we have the information below.
For the second disk, we have the information below.
(The minus sign indicates counterclockwise while the positive indicates clockwise.)
To do this problem, we use conservation of angular momentum. Before the disks are put in contact, the initial total angular momentum is given by the equation below.
It is just the sum of the angular momentums of each disk. When the disks are combined together, then final angular momentum can be found by the following equation.
Set this equal to the initial angular momentum.
Simplify and solve for 
Example Question #2 : Using Angular Momentum Equations
A piece of space debris is travelling in an elliptical orbit around a planet. At its closest point to the planet, the debris is travelling at 


The equation for conservation of angular momentum is:
This means that the angular momentum of the object at the two points in its orbit must be the same. Since the mass of the debris does not change, this gives us an equality of the product of the velocity and distance of the debris at any two points of its orbit:

Plug in known values.
There is disagreement between units; the velocities are given in both 

Solve for 
Example Question #1 : Interpreting Rotational Motion And Torque Diagrams
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
Pulling or pushing at an angle that is less perpendicular to the wrench
Increasing the magnitude of the force he puts on the wrench
Using a wrench of a different material
Using a longer wrench
Pulling or pushing at an angle that is more perpendicular to the wrench
Pulling or pushing at an angle that is less perpendicular to the wrench
Remember the torque equation:
Exerting force on the wrench at an angle less perpendicular to the wrench will reduce 
The other answer options will all increase the torque being applied, making the twisting motion easier.
Example Question #151 : Mechanics Exam
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Example Question #1 : Circular Motion
In uniform circular motion, the net force is always directed ___________.
away from the center of the circle
nowhere; the net force will be zero
in the same direction as the tangential velocity
toward the center of the circle
toward the center of the circle
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Example Question #1 : Circular Motion
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Example Question #232 : Ap Physics C
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
All AP Physics C: Mechanics Resources