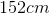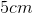Lenses
Help Questions
AP Physics 2 › Lenses
A 







Explanation
In order to solve this problem, we first must find where the image is located, and then we can use that to find the image's height.
The formula needed is:



In this case we have
We get
Now we can use the formula


to find the height of the image.
This means the image height is 

Suppose that an object is located 

The image will be virtual and up-right
The image will be real and up-right
The image will be virtual and upside down
The image will be real and upside down
Cannot be determined without knowing the height of the object
Explanation
In this question, we're presented with a scenario in which an object is placed a certain distance in front of a thin convex lens. After being given the radius of curvature for this lens, we're asked to determine certain properties of the image; whether it will be real or virtual and whether it will be up-right or upside down.
To begin with, let's use the following equation:
Where 


In order to calculate the focal length, we'll need to use the radius of curvature. The focal length is simply half this value:
Now that we have the focal length, we can calculate the image distance by first isolating the term:
Next, we can plug in values to obtain the image distance:
The value that we have obtained for the image distance is negative. This means that the image formed in this scenario will be a virtual image.
Moving forward, we can use the image distance and object distance in order to determine the orientation of the image (the magnification):
Since the value we obtained is positive, we can conclude that the image will be formed up-right.
A ray of light passes through the focal point and then strikes a thin lens. After refraction, this ray:
Emerges from the lens parallel to the principal axis
Appears to pass through the center of the lens
Passes through or appears to pass through the focal point
Passes through both the center of the lens and the focal point
The ray will be completely reflected and not refract through the lens
Explanation
One of the rules of drawing ray diagrams is that if the ray goes through the focal point on one side and hits a thin lens, then the ray will emerge parallel to the principal axis.
Two small blue LEDs, both with a wavelength of 



Not enough information to solve the problem.
Explanation
A telescope with an objective lens with a diameter 


The separation distance between the two objects, we will call this 

You are far away from the lights and this angle is very small so the small angle approximation can be used,
Setting these expressions for 



How will the image of an object appear if it is located outside the focal length of a converging lens?
Real and inverted
Real and upright
Virtual and upright
Virtual and inverted
Impossible to determine
Explanation
This question is asking us to determine the properties of the image formed by a converging lens when the object is located at a distance that is beyond the focal point of the lens.
One way to go about solving this problem is to draw a visual diagram showing ray vectors, as shown below.

In the above diagram, we have an object located on a flat surface, along with a converging lens to the right of it and the focal points on either side of the lens. After drawing these in, we need to draw our light rays as coming from the top of the object, and we'll need to use a total of three lines.
The first line is drawn horizontally from the top of the object to the middle of the lens. From there, this line is drawn passing through the focal point on the right.
The second line drawn is on the bottom in the picture above. This line is drawn from the top of the object and through the left focal point until it reaches the middle of the lens. From there, the ray is drawn from the middle of the mirror and straight horizontally.
Finally, the third line is drawn from the top of the object and through the very center of the lens.
At the point where all three of these lines intersect is where we will find the top of the image. As can be seen above, the top of the image will be facing downwards, and is therefore inverted.
To determine if the image is real or virtual, we have to ask ourselves: Are the light rays going where they're supposed to go, or did we have to extrapolate the rays to find our image? In this case, the rays went where they are supposed to go, which is through the lens and to the opposite side. Therefore, the image formed is real.