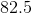Variable Relationships
Help Questions
Algebra 2 › Variable Relationships





Explanation
1. Since 


2. Solve for K using the x and y values given:
3. Use the equation you solved for to find the value of y:





Explanation
1. Since 


2. Solve for K using the x and y values given:
3. Use the equation you solved for to find the value of y:
The output of a factory in units per day versus the number of employees working is plotted on the graph below, with the following data points collected:
(Workers, Units of output per day):
Assuming a linear relationship, interpolate to find how many units will be made per day if 

Explanation
We want to do a linear interpolation since the relationship between workers and units can be assumed to be linear. This means there is a constant slope between the points, so the slope between two known points will be equal to the slope between the point we are trying to find and some known point. This is expressed in the relation:

where 





Plugging these into our interpolation formula and knowing 


Simplifying and rearranging to solve for 

So there are 






Explanation
1. Since 

2. Use the given x and y values to determine the value of K:
3. Using the equation along with the value of K, find the value of y when x=5:
The output of a factory in units per day versus the number of employees working is plotted on the graph below, with the following data points collected:
(Workers, Units of output per day):
Assuming a linear relationship, interpolate to find how many units will be made per day if 

Explanation
We want to do a linear interpolation since the relationship between workers and units can be assumed to be linear. This means there is a constant slope between the points, so the slope between two known points will be equal to the slope between the point we are trying to find and some known point. This is expressed in the relation:

where 





Plugging these into our interpolation formula and knowing 


Simplifying and rearranging to solve for 

So there are 






Explanation
1. Since 

2. Use the given x and y values to determine the value of K:
3. Using the equation along with the value of K, find the value of y when x=5:
What is the next number in this sequence: 8, 27, 64, 125 ?
Explanation
Find the pattern of the sequence:
This pattern is 
What is the next number in this sequence: 8, 27, 64, 125 ?
Explanation
Find the pattern of the sequence:
This pattern is 
Given the two following points, use interpolation to determine the best estimate for the value

Explanation
Using our two known points, we can use interpolation to determine the value at any point between them with the following formula:
Where 


Find the next 2 numbers in this sequence: 33, 46, 72, 111
Explanation
Find the pattern in this sequence of numbers:
In this case, the pattern is adding 13n to the previous number where n= how many numbers came before the current number.
so the first number we are looking for would be:
the second number we are looking for would be: