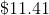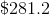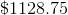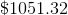How to find compound interest
Help Questions
ACT Math › How to find compound interest
If an account has interest compounded quarterly at an annual rate of 


Explanation
Recall that the equation for compounded interest (with quarterly compounding) is:
Where 



Thus, for our data, we need to know:
This is approximately 
If an account has interest compounded annually at a rate of 


Explanation
Recall that the equation for compounded interest (with annual compounding) is:
Where 


Thus, for our data, we need to know:
This is approximately 
Alice wants to invest money such that in 


Explanation
The formula for compound interest is
where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.
In this problem, we are solving for the principal, P. The given variables from the problem are:
Plugging these into the equation above, we get
Solving for P, we get
An account is compounded at a given rate of interest annually for 


Explanation
Recall that the equation for compounded interest (with annual compounding) is:
Where 


Thus, for our data, we need to know:
Now, let's use 

Using a logarithm, this can be rewritten:
This can be rewritten:
Now, you can solve for 
or
Now, finally you can rewrite this as:
Thus,
Now, round this to 
Thus, 

If an account has interest compounded annually at a rate of 


Explanation
Recall that the equation for compounded interest (with annual compounding) is:
Where 


Thus, for our data, we need to know:
This is approximately 
Michelle makes a bank deposit of $1,500 at 4.2% annual interest, compounded monthly. Approximately how much money will be in Michelle’s bank account in 3 years?
$1,693
$1,695
$1,697
$1,701
Explanation
The formula to use for compounded interest is
where P is the principal (original) amount, r is the interest rate (expressed in decimal form), n is the number of times per year the interest compounds, and t is the total number of years the money is left in the bank. In this problem, P=1,500, r=0.042, n=12, and t=3.
By plugging in, we find that Michelle will have about $1,701 at the end of three years.
If a cash deposit account is opened with 

Explanation
It is easiest to break this down into steps. For each year, you will multiply by 
After year 1: 
After year 2: 

After year 3: 

Thus, the positive difference of the interest from the last period and the interest from the first period is:
A five-year bond is opened with 

Explanation
Each year, you can calculate your interest by multiplying the principle (

For two years, it would be:

Therefore, you can solve for a five year period by doing:
Using your calculator, you can expand the 


Ashley makes a bank deposit of 







Explanation
The formula for compound interest is
where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.
In this problem, we are solving for time, t. The given variables from the problem are:
Plugging these into the equation above, we get
This simplifies to
We can solve this by taking the natural log of both sides
Jack has 



Explanation
First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).
Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:
Plug in the values given:
Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:
Add the two together, and we see that Jack makes a total of,