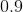All ACT Math Resources
Example Questions
Example Question #11 : Decimals
Find the square of 
Squaring a decimal is identical to multiplying decimals.
Drop the decimal, multiply the number by its self, and then add up the decimal points in the original problem and put it back into your answer.

Example Question #12 : Decimals
What is 
You can solve this on your calculator, or think about it as a fraction 

Example Question #1 : How To Square A Decimal
If 


First, we must figure out what 
We do 
Now to find out what 

We move our decimal points over so that we are dealing with only whole numbers. This gives us 
Finally, we count how many spaces we moved our decimals in total, and we move the decimal in our answer back that many spaces. To get from 



Therefore, we must take 


Example Question #3 : Basic Squaring / Square Roots
Evaluate the following:
To solve, simply multiply 0.02 by 0.02 as though the numbers are without decimals.
Then, sum the number of spaces to the right of the decimal points in your problem and include that many in your answer.
Thus, your answer is .0004.
Example Question #3 : Basic Squaring / Square Roots
Find the square root of the following decimal:
The easiest way to find the square root of a fraction is to convert it into scientific notation.
The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8
Example Question #22 : Decimals
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #2 : Basic Squaring / Square Roots
Find the square root of the following decimal:
This problem can be solve more easily by rewriting the decimal into scientific notation.
Because 
Example Question #3 : Basic Squaring / Square Roots
Find the square root of the following decimal:
This problem becomes much simpler if we rewrite the decimal in scientific notation
Because 
Example Question #1 : How To Find The Square Root Of A Decimal
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 
Example Question #22 : Decimals
Find the square root of the following decimal:
To find the square root of this decimal we convert it into scientific notation.
Because 


Certified Tutor
All ACT Math Resources