Calculating the length of the diagonal of a quadrilateral
Help Questions
GMAT Quantitative › Calculating the length of the diagonal of a quadrilateral
What is the length of the diagonal for a square with a side length of 
Explanation
The diagonal of a square is simply the hypotenuse of a right triangle whose other two sides are the length and width of the square. Because all sides of a square are equal in length, this means the length and width are both 


So the length of the diagonal for a square with a side length of 



Rhombus 


Explanation
A rhombus has four sides of equal length. Since Rhombus 





Rhombus 




None of the other choices gives a correct answer.
Explanation
The area of a rhombus is half the product of the lengths of its diagonals, which here are 

Since both diagonals have whole numbers as their lengths, and 


The quotient is
Since we can multiply both sides by 

we know that

so we can eliminate 12 and 16.
Also, since 

If 


Given the area of a square is 
Explanation
Write the formula for finding the area of a square given the diagonal.
Rearrange the equation so that the diagonal term is isolated.
Substitute the known area and simplify.
Calculate the length of the diagonal for a rectangle with a length of 

Explanation
The diagonal of a rectangle can be thought of as the hypotenuse of a right triangle whose base and height are the length and width of the rectangle, respectively. This means we can use the Pythagorean Theorem to calculate the length of the diagonal for a rectangle:
While walking with some friends on campus, you come across an open grassy rectangular area. You shout "Pythagoras!" and run across the rectangular area from one corner to another. If the rectangle measures 

Explanation
This problem can be solved in a variety of ways, however you do it, it may be worth eliminating any options shorter than either side of the quad. The diagonal distance is the hypotenuse of a triangle, so it must be longer than 25 or 60 meters.
Then, we can either find our hypotenuse via Pythagorean Theorem, or our knowledge of Pythagorean Triples.
Using Pythagorean Theorem:
So 65 meters.
Alternatively, recognize the triangle as a 5x/12x/13x triangle

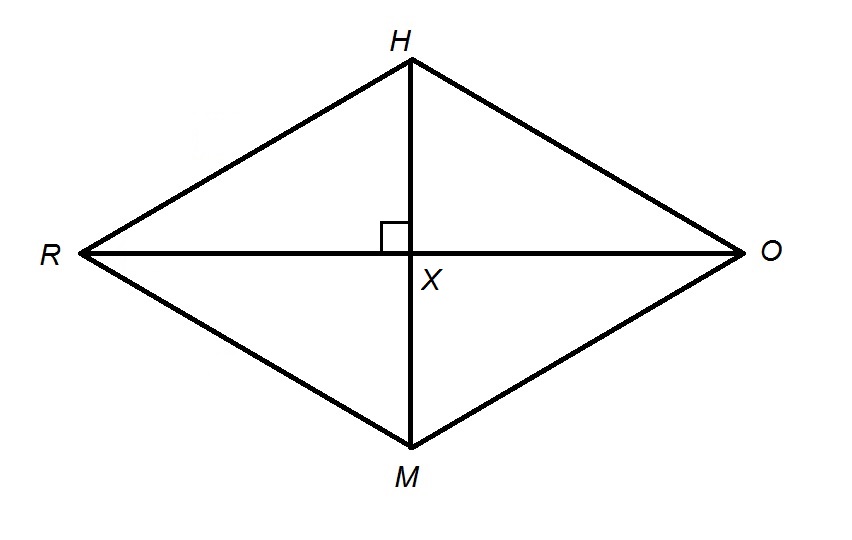
Given: Quadrilateral 





Give the length of diagonal 
None of the other responses is correct.
Explanation
The Quadrilateral 


. We call the point of intersection 

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, 







By the 30-60-90 Theorem, since 


By the 45-45-90 Theorem, since 


The diagonal 

Rhombus 


Explanation
The referenced rhombus, along with diagonals 

The four sides of a rhombus have equal measure, so each side has measure one fourth of the perimeter of 48, which is 12.
Since consecutive angles of a rhombus, as with any other parallelogram, are suplementary, 








and

Since the diagonals of a rhombus bisect each other, 
Rhombus 


Explanation
The sides of a rhombus are all congruent; since the perimeter of Rhombus 
The referenced rhombus, along with diagonal 

Since consecutive angles of a rhombus, as with any other parallelogram, are supplementary, 






Rhombus 
Which of the following could be true about the values of 

None of the other responses gives a correct answer.
Explanation
The area of a rhombus is half the product of the lengths of its diagonals, which here are 

Therefore, we need to test each of the choices to find the pair of diagonal lengths for which this holds.

Area:
Area:
Area:
Area:








































































