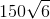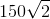How to find the area of an equilateral triangle
Help Questions
SSAT Upper Level Quantitative › How to find the area of an equilateral triangle
An equilateral triangle is circumscribed about a circle of radius 16. Give the area of the triangle.
The correct answer is not among the other choices.
Explanation
The circle and triangle referenced are below, along with a radius to one side and a segment to one vertex:





In the above diagram, 
The correct answer is not among the other responses.
Explanation
The interior angles of an equilateral triangle all measure 60 degrees, so, by the 30-60-90 Theorem,
Also, 


The area of this triangle is half the product of the base 

This answer is not among the given choices.
The perimeter of an equilateral triangle is 
Explanation
An equilateral triangle with perimeter 54 has three congruent sides of length
The area of this triangle is
The perimeter of an equilateral triangle is 
Explanation
An equilateral triangle with perimeter 
The area of this triangle is
An equilateral triangle has side lengths of 
Explanation
The area of an equilateral triangle can be found using this formula:
Using 
Hexagon 

Explanation
Since the perimeter of the (six-congruent-sided) regular hexagon is 72, each side has length one sixth this, or 12.
The figure described is given below, with a perpendicular segment drawn from 


Each angle of a regular hexagon measures 


By the 30-60-90 Theorem,
and



An equilateral triangle is inscribed inside a circle of radius 
Explanation
The trick is to know that the circumscribed circle, or the circumcircle, has as its center the intersection of the three altitudes of the triangle, and that this center, or circumcenter, divides each altitude into two segments, one twice the length of the other - the longer one being a radius. Because of this, we can construct the following:

Each of the six smaller triangles is a 30-60-90 triangle, and all six are congruent.
We will find the area of 
By the 30-60-90 Theorem, 


Six times this -