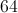All SSAT Middle Level Math Resources
Example Questions
Example Question #4 : How To Find Median
Find the median of this set of numbers:
753, 159, 456, 654, 852, 963, 741.
First, order the numbers from least to greatest.
Then, identify the middle number:
Example Question #1 : How To Find Median
Find the median of this set of numbers:
60, 74, 51, 43, 91,62, 65
First, place the numbers in order from least to greatest:
Then, identify the middle number: 62.
Example Question #2 : How To Find Median
Give the median of the following nine scores:
Arrange the scores from least to greatest.
There are an odd number (nine) of scores, so the median of the scores is the one that falls in the center - namely, 72.
Example Question #3 : How To Find Median
What is the median of the following set of numbers:
No number is the median for this set of numbers
The median is the number with an equal number of other items both above and below it. There are 9 total numbers in the list, 4 of them are below 7, and 4 of them are above 7.
Example Question #131 : Data Analysis And Probability
What is the median of the values 




The median of a set of values is the value that is in the middle when you rearrange the values from least to greatest. In this set, the values can be rearranged as 





Example Question #1 : Median
On a math test that the teacher gave her students, the scores were as follows:
What was the median score?
The median is the middle number in a set when the set of numbers is ordered sequentially.
When the intial set is reordered sequentially, you get the bottom set. (The top set is the original ordering of the numbers.)
In this sequential set of 7 numbers, the number 89 is in the fourth posiiton and exactly in the middle. Therefore, it is the mean.
Example Question #4 : How To Find Median
What is the median of this set of numbers?
To find the median of a set of numbers, you must first reorder them from smallest to largest. Below is the set reordered as such:
The median is the middle number of the set. Here, 57 is the middle number. Therefore, it is the median and the correct answer.
Example Question #132 : Data Analysis And Probability
Subtract the mode from the median in this set of numbers:
9080, 9008, 9800, 9099, 9009, 9090, 9008
First, order the numbers from least to greatest:
Then, find the mode (the most recurring number): 9008
Then, find the median (the middle number):
Finally, subtract the mode from the median:
Answer: 72.
Example Question #1 : Median
Consider the data set:
What is the difference between the mean of this set and the median of this set?
To get the mean, add the numbers and divide by 8:
To get the median, find the mean of the fourth- and fifth-highest elements (the ones in the middle):
The difference is
Example Question #461 : Data Analysis
In Jane's previous six basketball games, she made the following number of baskets:
What is the median number of baskets she made?
The first step to finding the median is to reorder the number of baskets that Jane scored from smallest to largest. This gives us:
The median number is the number in the middle of the set. Given that there are two middle numbers (4 and 6), the average of these numbers will be the median.
The average of 4 and 6 is:
Certified Tutor
All SSAT Middle Level Math Resources