All SAT Math Resources
Example Questions
Example Question #1 : How To Find The Answer To An Arithmetic Sequence
-27, -24, -21, -18…
In the sequence above, each term after the first is 3 greater than the preceding term. Which of the following could not be a value in the sequence?
126
657
461
501
461
All of the values in the sequence must be a multiple of 3. All answers are multiples of 3 except 461 so 461 cannot be part of the sequence.
Example Question #2 : How To Find The Answer To An Arithmetic Sequence
m, 3m, 5m, ...
The first term in the above sequence is m, and each subsequent term is equal to 2m + the previous term. If m is an integer, then which of the following could NOT be the sum of the first four terms in this sequence?
16
48
-32
80
60
60
The fourth term of this sequence will be 5m + 2m = 7m. If we add up the first four terms, we get m + 3m + 5m + 7m = 4m + 12m = 16m. Since m is an integer, the sum of the first four terms, 16m, will have a factor of 16. Looking at the answer choices, 60 is the only answer where 16 is not a factor, so that is the correct choice.
Example Question #1 : Other Arithmetic Sequences
The tenth term in a sequence is 40, and the twentieth term is 20. The difference between consequence terms in the sequence is constant. Find n such that the sum of the first n numbers in the sequence equals zero.
Let d represent the common difference between consecutive terms.
Let an denote the nth term in the sequence.
In order to get from the tenth term to the twentieth term in the sequence, we must add d ten times.
Thus a20 = a10 + 10d
20 = 40 + 10d
d = -2
In order to get from the first term to the tenth term, we must add d nine times.
Thus a10 = a1 + 9d
40 = a1 + 9(-2)
The first term of the sequence must be 58.
Our sequence looks like this: 58,56,54,52,50…
We are asked to find the nth term such that the sum of the first n numbers in the sequence equals 0.
58 + 56 + 54 + …. an = 0
Eventually our sequence will reach zero, after which the terms will become the negative values of previous terms in the sequence.
58 + 56 + 54 + … 6 + 4 + 2 + 0 + -2 + -4 + -6 +….-54 + -56 + -58 = 0
The sum of the term that equals -2 and the term that equals 2 will be zero. The sum of the term that equals -4 and the term that equals 4 will also be zero, and so on.
So, once we add -58 to all of the previous numbers that have been added before, all of the positive terms will cancel, and we will have a sum of zero. Thus, we need to find what number -58 is in our sequence.
It is helpful to remember that an = a1 + d(n-1), because we must add d to a1 exactly n-1 times in order to give us an. For example, a5 = a1 + 4d, because if we add d four times to the first term, we will get the fifth term. We can use this formula to find n.
-58 = an = a1 + d(n-1)
-58 = 58 + (-2)(n-1)
n = 59
Example Question #3 : How To Find The Answer To An Arithmetic Sequence
The first term of a sequence is 1, and every term after the first term is –2 times the preceding term. How many of the first 50 terms of this sequence are less than 5?
27
16
8
54
64
27
We can see how the sequence begins by writing out the first few terms:
1, –2, 4, –8, 16, –32, 64, –128.
Notice that every other term (of which there are exactly 50/2 = 25) is negative and therefore less than 25. Also notice that after the fourth term, every term is greater in absolute value than 5, so we just have to find the number of positive terms before the fourth term that are less than 5 and add that number to 25 (the number of negative terms in the first 50 terms).
Of the first four terms, there are only two that are less than 5 (i.e. 1 and 4), so we include these two numbers in our count: 25 negative numbers plus an additional 2 positive numbers are less than 5, so 27 of the first 50 terms of the sequence are less than 5.
Example Question #161 : Integers
Look for cancellations to simplify. The sum of all consecutive integers from 







Example Question #12 : Sequences
Brad can walk 3600 feet in 10 minutes. How many yards can he walk in ten seconds?
If Brad can walk 3600 feet in 10 minutes, then he can walk 3600/10 = 360 feet per minute, and 360/60 = 6 feet per second.
There are 3 feet in a yard, so Brad can walk 6/3 = 2 yards per second, or 2 x 10 = 20 yards in 10 seconds.
Example Question #5 : How To Find The Answer To An Arithmetic Sequence
The first, third, fifth and seventh terms of an arithmetic sequence are 




The first important thing to note is that the way these answer choices are set up, any answer that does not have a 


Example Question #8 : Other Arithmetic Sequences
Find the unknown term in the sequence:
The pattern in this sequence is 



Then, our third term must be:

Example Question #21 : Sequences
An arithmetic sequence begins as follows:
Give the first integer in the sequence.
The sequence has no integers.
The sequence has no integers.
Rewrite all three fractions in terms of their least common denominator, which is 


The sequence begins
Subtract the first term 


Setting 

If this common difference is added a few more times, a pattern emerges:

All of the denominators end in 4 or 9, so none of them can be divisible by 20. Therefore, none of the terms will be integers.
Example Question #21 : Sequences
An arithmetic sequence begins as follows:
What is the first positive number in the sequence?
The twenty-third term
The twentieth term
The nineteenth term
The twenty-second term
The twenty-first term
The twentieth term
Given the first two terms 


Setting 

The 
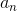
Since we are looking for the first positive number - equivalently, the first number greater than 0:


Setting 


Since 



Certified Tutor
Certified Tutor
All SAT Math Resources

















































