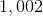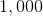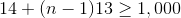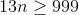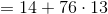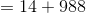Arithmetic
Help Questions
SAT Math › Arithmetic
The price of a computer is reduced by 1/8. The new price is then reduced by 1/6. What fraction of the original price is the current price?
1/48
1/24
35/48
23/24
13/48
Explanation
Let the original price = p.
After the first reduction, the price is (7/8)p
After the second reduction, the price is (5/6)(7/8)p = (35/48)p
Write 7.5% as a fraction.
Explanation
First convert the percentage to a decimal:
7.5% = .075
Then turn this into a fraction:
.075 = 75/1000
Simplify by dividing the numerator and denominator by 25:
75/1000 = 3/40
Order these decimals from greatest to least:
Explanation
Ordering decimals from greatest to least means we list them from the biggest number to the smallest number. When doing this, line up each of your numbers by their decimal points. We look at the tenths place first and order them according to that number. Then move on to the hundredths place and so on until each of the numbers are lined up from greatest to smallest. For this problem that would look like this:
Find the decimal equivalent to the percentage:
Explanation
In order to find the decimal equivalent of a percentage, the number that makes up the percent has to be divided by 100. However, since it is division by a power of 10, we can accomplish the same thing, by moving the decimal point 2 places to the left, thus making the number smaller. For this problem, that looks like this:
An arithmetic sequence begins as follows: 14, 27, 40...
What is the first four-digit integer in the sequence?
Explanation
Given the first two terms 


Setting 

The 
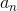
Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:
Setting 


Therefore, the 77th term, or 




the correct choice.
An arithmetic sequence begins as follows:
Give the first integer in the sequence.
The sequence has no integers.
Explanation
Subtract the first term 


Setting 

If 


Solving for 
Therefore, we seek the least positive integer value of 



which is an integer.
Therefore, 2 is the first integer value in the sequence.
Turn the following percentage into a fraction:
Explanation
Since a percentage is a "part of 100" to turn it into a fraction we take the original number in the percent and place it over 100:
From here, simplify the fraction as necessary:
Round 901,527 to the nearest thousand and convert to scientific notation.
Explanation
When rounding to the nearest thousand, look to the hundreds place to determine whether you need to round up or down. You always round down when the digit is between 0 and 4, and up when it is between 5-9. Therefore, the rounded number is 902,000. When using scientific notation, the first number in the notation must be less than 10. In this case, that number is 9.
From there, the decimal goes immediately after. Then count how many places the decimal would have to be moved in order to convert back to the original number (5 places).
When the decimal is moved to the left when writing it in scientific notation, the exponent is positive. When moved to the right to write the number in scientific notation, the exponent is negative.
If a car travels at 30 mph, how many feet per second does travel?
44 ft/s
2,640 ft/s
4,400 ft/s
440 ft/s
264 ft/s
Explanation
30 miles / 1 hour * 5280 ft / 1 mile * 3600 seconds / 1 hour = 44 ft/sec
4/5 + 7/3 + 9/30 = ?
103 / 30
20 / 38
20 / 30
80 / 30
30 / 100
Explanation
To add fractions you must first find the lease common denominator, that is, a number that all of the denominators (the bottom number) can divide into.
In this case, 5, 3, and 30, both 5 and 3 divide successfully into 30, so 30 is the least common denominator.
Now divide each smaller denominator into thirty. Then multiple the answer by the top number:
5/30 = 6
Therefore 4/5 = 4*6 / 5*6 = 24/30
3/30 = 10
Therefore 7*10 / 3*10 = 70/30
Then add all the numerators together:
24/30 + 70/30 +9/30 = (24+70+9)/30 = 103 / 30