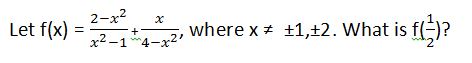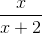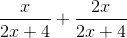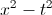Rational Expressions
Help Questions
SAT Math › Rational Expressions
9/5
–37/15
–11/5
37/15
–9/5
Explanation
9/5
–37/15
–11/5
37/15
–9/5
Explanation
Simplify the expression.
Explanation
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
This is the most simplified version of the rational expression.
Simplify the expression.
Explanation
To add rational expressions, first find the least common denominator. Because the denominator of the first fraction factors to 2(x+2), it is clear that this is the common denominator. Therefore, multiply the numerator and denominator of the second fraction by 2.
This is the most simplified version of the rational expression.
Which of the following is equivalent to 
Explanation
We will need to simplify the expression 


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

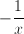


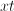
In order to convert the fraction 
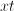

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction 

To simplify this further, we can think of 


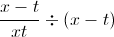
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
Which of the following is equivalent to 
Explanation
We will need to simplify the expression 


In order to simplify the numerator, we will need to combine the two fractions. When adding or subtracting fractions, we must have a common denominator. 

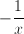


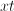
In order to convert the fraction 
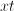

Similarly, we will multiply the top and bottom of 

We can now rewrite 

Let's go back to the original fraction 

To simplify this further, we can think of 


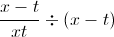
Lastly, we will use the property of exponents which states that, in general, 
The answer is 
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
(4x2 + 8x)/(x4 + 8x)
x/(x – 2)2
4/(x – 2)2
x/(x + 2)
4/(x + 2)2
Explanation
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
Simplify (4x)/(x2 – 4) * (x + 2)/(x2 – 2x)
(4x2 + 8x)/(x4 + 8x)
x/(x – 2)2
4/(x – 2)2
x/(x + 2)
4/(x + 2)2
Explanation
Factor first. The numerators will not factor, but the first denominator factors to (x – 2)(x + 2) and the second denomintaor factors to x(x – 2). Multiplying fractions does not require common denominators, so now look for common factors to divide out. There is a factor of x and a factor of (x + 2) that both divide out, leaving 4 in the numerator and two factors of (x – 2) in the denominator.
what is 6/8 X 20/3
5
120/11
18/160
9/40
3/20
Explanation
6/8 X 20/3 first step is to reduce 6/8 -> 3/4 (Divide top and bottom by 2)
3/4 X 20/3 (cross-cancel the threes and the 20 reduces to 5 and the 4 reduces to 1)
1/1 X 5/1 = 5
Simplify the following rational expression: (9x - 2)/(x2) MINUS (6x - 8)/(x2)
Explanation
Since both expressions have a common denominator, x2, we can just recopy the denominator and focus on the numerators. We get (9x - 2) - (6x - 8). We must distribute the negative sign over the 6x - 8 expression which gives us 9x - 2 - 6x + 8 ( -2 minus a -8 gives a +6 since a negative and negative make a positive). The numerator is therefore 3x + 6.