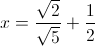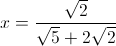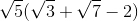All SAT Math Resources
Example Questions
Example Question #1 : Basic Squaring / Square Roots
Solve for 
Notice how all of the quantities in square roots are divisible by 9
Simplifying, this becomes
Example Question #1 : Basic Squaring / Square Roots
Solve for 
Note that all of the square root terms share a common factor of 36, which itself is a square of 6:
Factoring 
Example Question #2 : Basic Squaring / Square Roots
Solve for 
Note that both 



From here, we can factor 
Example Question #2 : Basic Squaring / Square Roots
Solve for 
In order to solve for 
Simplifying, this becomes:
Example Question #1 : Factoring Common Factors Of Squares And Square Roots
Which of the following is equivalent to:

To begin with, factor out the contents of the radicals. This will make answering much easier:
They both have a common factor 
This is the same as:
These have a common 
Example Question #2 : Basic Squaring / Square Roots
Simplify:
These three roots all have a 
Now, this could be rewritten:
Now, note that
Therefore, you can simplify again:
Now, that looks messy! Still, if you look carefully, you see that all of your factors have 
This is the same as:
Example Question #4 : Basic Squaring / Square Roots
Solve for 
Examining the terms underneath the radicals, we find that 







The equation can then be expressed in terms of these factored radicals as shown:


Factoring the common term 
Divide both sides by the expression in the parentheses:
Divide both sides by 

Simplify the fraction on the righthand side by dividing the numerator and denominator by 
This is the solution for the unknown variable 
Certified Tutor
Certified Tutor
All SAT Math Resources