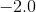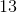All SAT Math Resources
Example Questions
Example Question #2 : How To Add Decimals

A family is taking a trip from Town A to Town B, then to Town C. Above is a diagram of the routes available to them.
Give the range for the driving distance 
None of the other choices gives the correct response.
Each route includes one path from Point A to Point B and one path from Point B o Point C.
The shortest possible drive is the sum of the shortest paths for each leg of the trip:
The longest possible drive is the sum of the longest paths for each leg of the trip:
The correct response is that 
Example Question #3 : How To Add Decimals

Above is a simplified map of the routes from Town A to Town B, and the routes from Town B to Town C.
A family wants to travel from Town A to Town C by way of Town B, then back to Town A by way of Town B. Since all routes are scenic, the family does not want to take any route twice.
Give the range for the distance 
The family's trip will be designed so that the family will take two different routes of the three that connect Town A and Town B, and two different routes of the three that connect Town B and Town C.
The minimum distance that the family will travel is therefore the sum of the lengths of the two shortest routes from Town A to Town B, and those of the two shortest routes from Town B to Town C:

The maximum distance that the family will travel is, similarly, the sum of the lengths of the two longest routes from Town A to Town B, and those of the two longest routes from Town B to Town C:

The correct choice is therefore 
Example Question #4 : How To Add Decimals

A family is taking a trip from Town A to Town B, then to Town C. Above is a diagram of the routes available to them. How many routes will only require them to drive 40 miles or fewer:
Five
Six
Two
Three
Four
Five
There are three routes from Point A to Point B, and three from Point B to Point C, for a total of 
Five of these routes require driving a distance 40 miles or fewer.
Example Question #413 : Arithmetic
Round the answer to the nearest tenth.
0.57 - 2.657 = -2.087
Don't forget the negative sign!
This number then rounds to -2.1.
Example Question #411 : Arithmetic
45.728 x 3.2 = ?
146.3296
14632.96
14.63296
146329.6
1463.296
146.3296
Multiply the numbers out in long format, then move the decimal point over the total number of decimal points in the two numbers (3 in the first, 1 in the second, so 4 total):
45.728 * 3.2 = 91456
91456 + 1371840 = 1,463,296 → 146.3296
Or just count the decimal points in the answer and make sure it's 4.
Example Question #414 : Arithmetic
At the farmer's market, oranges are $0.30 each, apples are $0.25 each, bananas are $0.40 each, and tomatoes are $0.60 each. If Scott buys 3 oranges, 7 apples, 4 bananas, and 8 tomatoes, how much does he spend?
$10.40
$6.80
$9.05
$7.75
$11.40
$9.05
To find out how much Scott spends, we need to multiply the quantity of each fruit by its price and add them all up.
3 * $0.30 + 7 * $0.25 + 4 * $0.40 + 8 * $0.60 = $9.05
Example Question #421 : Arithmetic
If 


We can approximate the value of y pretty quickly:
y ≈ 1(0.50)(52) = 26
Since y = 0.25x = (1/4)x we know that x = 4y ≈ 4(26) = 104
Example Question #422 : Arithmetic
0.0006
0.6
0.006
6
0.06
0.006
It's much easier to work with whole numbers, so we'll ignore the decimals for the first step: 5 x 12 = 60
Now look at the decimals. To add them back in, think of 60 as 60.0. Now move the decimal point four places to the left: 0.5 x 0.012 = .0060 = .006
Example Question #423 : Arithmetic
You bought a dozen eggs marked at 


Set the equation up as

Solve for 

or
Therefore the percent sales tax is:
Example Question #1 : How To Divide Decimals
simplify: 0.2 ÷ 0.04
0.2 ÷ 0.04 <- easiest way to approach is to move the decimal to the right (the same amount of spaces on each side) so that the decimal disappears
since 0.04 has 2 spaces and 0.2 only has 1, move the decimal 2 spaces to the right on each side
0.2 ÷ 0.04 = 20 ÷ 4 = 5
Certified Tutor
All SAT Math Resources