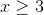All SAT II Math I Resources
Example Questions
Example Question #101 : Single Variable Algebra
Give the solution set of the inequality
Two numbers of like sign have a positive quotient.
Therefore, 


To find this set of points, we identify the zeroes of both expressions.
Since 



Choose 

Choose 

Choose 

The solution set is
Example Question #101 : Single Variable Algebra
Solve for x.
Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, add 7 to each side.
Now, divide both sides by 2.
Example Question #102 : Single Variable Algebra
Solve for x.
Solving inequalities is very similar to solving an equation. We must start by isolating x by moving the terms farthest from it to the other side of the inequality. In this case, subtract 2from each side.
Now, divide both sides by 2.
Example Question #105 : Single Variable Algebra
Solve the following inequality:
To solve for an inequality, you solve like you would for a single variable expression and get 
First, subtract 

Then divide both sides by 

Example Question #101 : Single Variable Algebra
Solve the inequality:
Simplify the left side.
The inequality becomes:
Divide by two on both sides.
The answer is:
Example Question #107 : Single Variable Algebra
Solve the inequality:
Subtract 
Add 3 on both sides.
Divide by 7 on both sides.
The answer is:
Certified Tutor
All SAT II Math I Resources