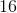Whole and Part
Help Questions
PSAT Math › Whole and Part
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
10
11
12
13
14
Explanation
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.
In the 30-day month of January, for every three days it snowed, there were seven days it did not snow. The number of days in January on which it did not snow was how much greater than the number of days in January on which it snowed?
10
11
12
13
14
Explanation
The question tells us that for every ten-day period in January (a three-day period plus a seven-day period), it snowed on 3 of those days and did not snow on 7 of those days. Since January has 30 days, it has 3 ten-day periods, so we multiply the numbers given for the 10-day period by 3 to find the number of days with and without snow during the 30-day period. Doing this, we see that it snowed 3 * 3 = 9 days and did not snow 7 * 3 = 21 days during the 30-day period. Since the question asks how much greater the number of days on which it did not snow is than the number of days on which it snowed, we subtract as follows: number of days it did not snow - number of days it snowed = 21 – 9 = 12.
A pitcher of water is filled 
45
30
35
40
50
Explanation
If 






If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
Explanation
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
A pitcher of water is filled 
45
30
35
40
50
Explanation
If 






If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
Explanation
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
$10.00
$6.50
$4.00
$2.50
$1.00
Explanation
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
Mr. Owens spent $7.50 for a dinner buffet. The amount he paid accounted for 3/4 of the money in his wallet. How much money is left in his wallet for other expenses?
$10.00
$6.50
$4.00
$2.50
$1.00
Explanation
If $7.50 is 3/4 of the total, 7.50/3 gives us what 1/4 of his total money would be. This equals $2.50, the remaining unspent quarter.
What is the remainder when 27 is divided by 6?
0.5
3
4
4.5
8
Explanation
Long division is the fastest way: 6 goes into 27 four times. 6 times four is 24. 27 – 24 = 3.
What is the remainder when 27 is divided by 6?
0.5
3
4
4.5
8
Explanation
Long division is the fastest way: 6 goes into 27 four times. 6 times four is 24. 27 – 24 = 3.