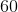All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Least Common Multiple
How many positive integers less than ten thousand are multiples of both eight and eighteen?
72
139
555
138
70
138
In order to find all of the numbers that are multiples of both 8 and 18, we need to find the least common mutliple (LCM) of 8 and 18. The easiest way to do this would be to list out the multiples of 8 and 18 and determine the smallest one that is common to both.
First, let's list the first several multiples of eight:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88 . . .
Next, we list the first several multiples of eighteen:
18, 36, 54, 72, 90, 108, 126, 144 . . .
By comparing the multiples of eight and eighteen, we can see that the smallest one that they share is 72. Thus, the LCM of 8 and 18 is 72.
Because the LCM is 72, this means that every multiple of 72 is also a multiple of both 8 and 18. So, in order to find all of the multiples less than ten thousand that are both multiples of 8 and 18, we simply need to find how many multiples of 72 are less than 10000, and to do this, all we have to do is to divide 10000 by 72.
When we divide 10000 by 72, we get 138 with a remainder of 64; therefore, 72 will go into ten thousand 138 times before it exceeds ten thousand. In other words, there are 138 numbers less than 10000 that are multiples of 72 and, by extension, also multiples of both 8 and 18.
The answer is 138.
Example Question #1 : Factors / Multiples
If 

136
154
168
172
114
168
The simplest way to solve this question is to go through each answer choice and check to see if it is divisible by 2, 4 and 7. When we do this, we find that only 168 is evenly divisible by each of these numbers. 114 is not divisible by 4 or 7, 172 is not divisibly by 7, 136 is not divisble by 7, and 154 is not divisible by 4.
Example Question #2 : Factors / Multiples
If a, b, and c are positive integers such that 4a = 6b = 11c, then what is the smallest possible value of a + b + c?
132
33
121
67
11
67
We are told that a, b, and c are integers, and that 4a = 6b = 11c. Because a, b, and c are positive integers, this means that 4a represents all of the multiples of 4, 6b represents the multiples of 6, and 11c represents the multiples of 11. Essentially, we will need to find the least common multiples (LCM) of 4, 6, and 11, so that 4a, 6b, and 11c are all equal to one another.
First, let's find the LCM of 4 and 6. We can list the multiples of each, and determine the smallest multiple they have in common. The multiples of 4 and 6 are as follows:
4: 4, 8, 12, 16, 20, ...
6: 6, 12, 18, 24, 30, ...
The smallest multiple that 4 and 6 have in common is 12. Thus, the LCM of 4 and 6 is 12.
We must now find the LCM of 12 and 11, because we know that any multiple of 12 will also be a multiple of 4 and 6.
Let's list the first several multiples of 12 and 11:
12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, ...
11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, ...
The LCM of 12 and 11 is 132.
Thus, the LCM of 4, 6, and 12 is 132.
Now, we need to find the values of a, b, and c, such that 4a = 6b = 12c = 132.
4a = 132
Divide each side by 4.
a = 33
Next, let 6b = 132.
6b = 132
Divide both sides by 6.
b = 22
Finally, let 11c = 132.
11c = 132
Divide both sides by 11.
c = 12.
Thus, a = 33, b = 22, and c = 12.
We are asked to find the value of a + b + c.
33 + 22 + 12 = 67.
The answer is 67.
Example Question #281 : Arithmetic
If 
Since v is divisible by 2, 3 and 15, v must be a multiple of 30. Any number that is divisible by both 2 and 15 must be divisible by their product, 30, since this is the least common multiple.
Out of all the answer choices, v + 30 is the only one that equals a multiple of 30.
Example Question #1 : Greatest Common Factor
Suppose that 



We are given information that m/4 is 10 greater than m/3. We set up an equation where m/4 = m/3 + 10.
We must then give the m variables a common denominator in order to solve for m. Since 3 * 4 = 12, we can use 12 as our denominator for both m variables.
m/4 = m/3 + 10 (Multiply m/4 by 3 in the numerator and denominator.)
3m/12 = m/3 + 10 (Multiply m/3 by 4 in the numerator and denominator.)
3m/12 = 4m/12 + 10 (Subtract 4m/12 on both sides.)
-m/12 = 10 (Multiply both sides by -12.)
m = -120
-120/4 = -30 and -120/3 = -40. -30 is 10 greater than -40.
Example Question #1 : Factors / Multiples




Which of the following is a possible value of 
We need to find ways to factor 18 such that the three factors are different, and then find the sum of those factors in each case.
18 can be factored as the product of three integers in four ways:
I)
II)
III)
IV)
Disregard I and IV since each repeats a factor.
In (II), the sum of the factors is 

Example Question #3 : Factors / Multiples




Which of the following cannot be equal to 
We look for ways to write 45 as the product of three integers, then we find the sum of the integers in each situation. They are:
Sum:
Sum:
Sum:
Sum:
Of the five choices, only 33 is not a possible sum of the factors. This is the correct choice.
Example Question #6 : Factors / Multiples
What is the greatest common factor of 

The greatest common factor is the largest factor that both numbers share. Each number has many factors. The factors for 72 are as follows:
Starting from the largest factor, 72, we can see that it is also a factor of 144

Therefore, 72 is the greatest common factor.
Example Question #2 : Factors / Multiples



The greatest common divisor of 

The greatest common divisor of 

The greatest common divisor of 

If 
The greatest common divisor of 



The greatest common divisor of 



The greatest common divisor of 



Thus:
We substitute these equalities into the given expression and simplify.
Since 










Therefore:
or
Example Question #1 : Prime Numbers
The sum of the first seven prime numbers divided by two is
33
29
58
24
61
29
The first seven primes are 2, 3, 5, 7, 11, 13, and 17. Don't forget about 2, the smallest prime number, and also the only even prime! Adding these seven numbers gives a sum of 58, and 58/2 = 29.
All PSAT Math Resources