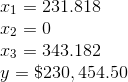All Math Modeling Resources
Example Questions
Example Question #2 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 510 acres of soy planted and 65 acres of oats.
The maximum profit at this solution will be, $223,500.
Example Question #7 : Math Modeling
A farm has 750 acres of land available for planting crops. The possible crops are soy, corn, and oats. There is 1,200 acre-ft of water for irrigation and the crew will be able to work of the farm 575 hours per week.
Find the amount of each crop that should be planted to maximize the profit.
The table below includes some additional, helpful information.
The objective of this particular problem is to maximize the profit.
Maximize the function:
over the region defined by the constraints.
First identify the variables and assumptions of the problem.

Now using the constraints formulate the linear programming model.
From here use computer implementation to solve using the simplex method.
Therefore, the optimal solution will occur when there are 343.182 acres of soy planted and 231.818 acres of corn planted.
The maximum profit at this solution will be, $230,454.50.
All Math Modeling Resources