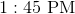All ISEE Upper Level Math Resources
Example Questions
Example Question #3 : How To Find The Area Of A Sector
While visiting a history museum, you see a radar display which consists of a circular screen with a highlighted wedge with an angle of 
While visiting a history museum, you see a radar display which consists of a circular screen with a highlighted wedge with an angle of 
To begin, let's recall our formula for area of a sector.
Now, we have theta and r, so we just need to plug them in and simplify!
So our answer is
Example Question #81 : Circles
A giant clock has a minute hand six feet long. How far, in inches, did the tip move between noon and 1:20 PM?
The distance that the tip of the minute hand moves during one hour is the circumference of a circle with radius 6 feet. This circumference is 



Example Question #1 : How To Find The Length Of An Arc
A giant clock has a minute hand three feet long. How far, in inches, did the tip move between noon and 12:20 PM?
It is impossible to tell from the information given
The distance that the tip of the minute hand moves during one hour is the circumference of a circle with radius 




Example Question #5 : Sectors

In the above figure, express 

The measure of an arc - 

Example Question #6 : Sectors

In the above diagram, radius 
Give the length of 
The circumference of a circle is 



The length of 


Example Question #5 : Sectors
While visiting a history museum, you see a radar display which consists of a circular screen with a highlighted wedge with an angle of 
While visiting a history museum, you see a radar display which consists of a circular screen with a highlighted wedge with an angle of 
To begin, let's recall our formula for length of an arc.
Now, just plug in and simplify
So, our answer is 4.54in
Example Question #1 : How To Find The Angle Of A Sector
A giant clock has a minute hand four feet long. Since noon, the tip of the minute hand has traveled 
The circumference of the path traveled by the tip of the minute hand over the course of one hour is:

Since the tip of the minute hand has traveled 


Example Question #1 : How To Find The Angle Of A Sector

Figure NOT drawn to scale
Refer to the above diagram.


An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, 




Inscribed 


The major arc corresponding to this minor arc, 
Example Question #222 : Geometry

Note: Figure NOT drawn to scale
Refer to the above diagram.

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, 

Inscribed 


Example Question #1 : How To Find The Angle Of A Sector

In the above diagram, radius 
Calculate the length of 
Inscribed 



This makes 
of the circle.
The circumference of a circle is 

The length of 


All ISEE Upper Level Math Resources