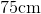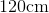All ISEE Upper Level Math Resources
Example Questions
Example Question #1 : Geometry
What is the sidelength, in feet and inches, of a regular hexagon with perimeter 16 feet?
Divide the perimeter 16 feet by 6 to get the sidelength of the hexagon in feet:
Two-thirds of a foot is equal to eight inches, so this sidelength is 2 feet 8 inches.
Example Question #1 : Geometry
The perimeter of a regular hexagon is one mile. Give the sidelength in feet.
One mile is equal to 5,280 feet, so divide this by 6:

Example Question #3 : Hexagons
A hexagon has a perimeter of 114in. Find the length of one side.
A hexagon has 6 equal sides. The formula to find perimeter of a hexagon is:
where a is the length of any side. Now, to find the length of one side, we will solve for a.
We know the perimeter of the hexagon is 114in. So, we will substitute and solve for a. We get
Therefore, the length of one side of the hexagon is 19in.
Example Question #3 : Plane Geometry
The perimeter of a hexagon is 96cm. Find the length of one side.
A hexagon has 6 equal sides. To find the length of one side of a hexagon, we will use the formula to find the perimeter.
where a is the length of one side. So, we will solve for a.
Now, we know the perimeter of the hexagon is 96cm. So, we get

Therefore, the length of one side of the hexagon is 16cm.
Example Question #1 : Plane Geometry
If the sum of 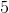
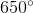
The sum of the angles in a polygon can be found using the equation below, in which t is equal to the total sum of the angles, and n is equal to the number of sides.
Given that a hexagon has 6 angles, the total number of angles will be:
Given that 5 of the angles have a sum of 650 degrees, we would subtract 650 from 720, resulting in 70 degrees.
Example Question #1 : Isee Upper Level (Grades 9 12) Mathematics Achievement
Find the perimeter of a hexagon with one side having a length of 15cm.
To find the perimeter of a hexagon, we will use the following formula:
where a is the length of one side of the hexagon.
Now, we know the length of one side of the hexagon is 15cm.
Knowing this, we can substitute into the formula. We get
Example Question #7 : Hexagons
Find the perimeter of a hexagon with a side having a length of 13cm.
A hexagon has 6 sides. So, to find the perimeter, we will use the following formula:
where a is the length of one side.
Now, we know a side has a length of 13cm. Knowing this, we can substitute into the formula.
Example Question #2 : Geometry
A hexagon has a side of length 13cm. Find the perimeter.
To find the perimeter of a hexagon, we will use the following formula:
where a is the length of one side of the hexagon. We multiply it by 6 because a hexagon has 6 equal sides.
So, we know the length of one side is 13cm. Knowing this, we can substitute into the formula. We get
Example Question #1 : Isee Upper Level (Grades 9 12) Mathematics Achievement
Find the perimeter of a hexagon with a side having a length of 12in.
To find the perimeter of a hexagon, we will use the following formula:
where a is the length of one side of the hexagon. Because a hexagon has 6 equal sides, we can use any side in the formula.
So, we know the length of one side is 12in. So, we can substitute. We get
Example Question #10 : Hexagons
Find the perimeter of a hexagon if it contains a side having a length of 17cm.
To find the perimeter of a hexagon, we will use the following formula:
where a is the length of one side of the hexagon.
Now, we know the length of one side of the hexagon is 17cm.
Knowing this, we can substitute into the formula. We get
All ISEE Upper Level Math Resources