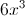All High School Math Resources
Example Questions
Example Question #2 : Equations
Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are 


What is the monthly break-even point?
The break-even point occurs when the 
The equation to solve becomes


Example Question #1 : Equations
Cindy's Cotton Candy sells cotton candy by the bag. Her monthly fixed costs are 


To make a profit of 
So the equation to solve becomes 


Example Question #3 : Equations
Solve for 







The two equations in this system can be combined by addition or subtraction to solve for 




Divide both sides by 


Substituting 




Example Question #2 : Basic Single Variable Algebra
Solve for 
Rewrite 
The solution set is
Example Question #6 : Equations



33
65
25
130
112
65
First, notice that we can factor 
If we divide both sides by 3, we can obtain the value of a+b.
We now have a system of equations: a-b = 3, a+b = 11. We will solve this system by elimination. If we add the two equations together, we obtain the following:

Divide both sides by 2.
Going back to the equation a-b = 7, we can solve for b.
Add b to both sides.
Subtract 3 from both sides.
Ultimately, the question asks us to determine the value of 


The answer is 65.
Example Question #201 : Algebra Ii
Solve the pair of equations for x and y:
Equation 1:
Equation 2:
Solve equation 2 for X:
Substitute into Equation 1:
Solve for y: 
Take the answer for y and plug it back into either original equation to find x:
Example Question #202 : Algebra Ii
Solve the pair of equations for x and y:
Equation 1:
Equation 2:
Solve Equation 2 for y:
Substitute into Equation 1:
Plug x back into either original equations and solve for y:
Example Question #203 : Algebra Ii
For which of the following functions is the result of 
Simply plugging in -2 into each answer choice will determine the correct answer:
The key to solving this problem is to remember the order of operations and that negative numbers squared are positive, while negative numbers raised to the third power are negative.
Example Question #1491 : High School Math
Given the equation 

8
4
18
15
12
15
When solving the equation 

Example Question #1492 : High School Math
A cardboard packing box contains footballs and baseballs. The ratio by weight of baseballs to footballs is 7 to 9. How many kilograms of footballs will there be in the box if the total weight of the box is 48 kilograms?
27
20
26
15
30
27
In the box, there are 




All High School Math Resources