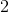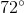All High School Math Resources
Example Questions
Example Question #1 : Trapezoids
Find the area of the following trapezoid:
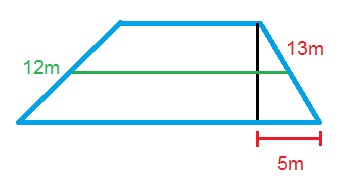
The formula for the area of a trapezoid is

Use the Pythagorean Theorem to find the length of the height:
Plugging in our values, we get:
Example Question #2 : How To Find The Area Of A Trapezoid
Find the area of the following trapezoid:

The formula for the area of a trapezoid is

where 

Use the formula for a 
Use the formula for a 
Plugging in our values, we get:
Example Question #1 : Trapezoids
What is the area of this regular trapezoid?

26
45
20
32
32
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
Example Question #2 : Trapezoids

What is the area of the trapezoid above if a = 2, b = 6, and h = 4?
16
64
24
8
32
16
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
Example Question #161 : Geometry
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by a2. Thus, the area of the square given in the problem is s2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = s2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2s2
Distribute the s on the left.
4s + s2 = 2s2
Subtract s2 from both sides.
4s = s2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.
Example Question #1 : How To Find The Area Of A Trapezoid
This figure is an isosceles trapezoid with bases of 6 in and 18 in and a side of 10 in.
What is the area of the isoceles trapezoid?
In order to find the area of an isoceles trapezoid, you must average the bases and multiply by the height.
The average of the bases is straight forward:
In order to find the height, you must draw an altitude. This creates a right triangle in which one of the legs is also the height of the trapezoid. You may recognize the Pythagorean triple (6-8-10) and easily identify the height as 8. Otherwise, use 

Multiply the average of the bases (12) by the height (8) to get an area of 96.

Example Question #1 : How To Find An Angle In A Trapezoid
Find the measure of angle 

The sum of the angles in any quadrilateral is 360°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360° gives the sum of the two top angles, and dividing the resulting 216° by 2 yields the measurement of x, which is 108°.
Example Question #1 : How To Find The Perimeter Of A Trapezoid
This figure is an isosceles trapezoid with bases of 6 in and 18 in and a side of 10 in.
What is the perimeter of the isoceles trapezoid (in.)?
The perimeter of the isoceles trapezoid is the sum of all the sides. You can assume the left side is also 10 in. because it is an isoceles trapezoid.
Example Question #14 : Quadrilaterals
Find the perimeter of the following trapezoid:

The formula for the perimeter of a trapezoid is:
Where 

Plugging in our values, we get:
Example Question #523 : High School Math
Find the perimeter of the following trapezoid:

Use the formula for 
The formula is:
Where 

Beginning with the 



Creating another 



The formula for the perimeter of a trapezoid is:
Where 

Plugging in our values, we get:
Certified Tutor
Certified Tutor
All High School Math Resources