All High School Math Resources
Example Questions
Example Question #11 : Algebra Ii
Expression 1:
Expression 2:
Find the set of values for 
All values where
All values where
All values where
All real numbers
All values where
All values where
In finding the values for 

The first possibility is described by the inequality:
If you think of a number line, it is evident that there is no solution to this inequality since there will never be a case where subtracting from 

The second possibility, wherein 

We can simplify this inequality to find that 

The third possibility can be represented by the following inequality (where the sign is inverted due to multiplication by a negative):
This is again simplified to 
The final possibility is represented by the inequality
This inequality simplifies to 

The only possible condition that satisfies the inequality is that which arises in two of the tested cases, when 
Example Question #1 : Understanding Absolute Value
What is the absolute value of -3?
1
3
10
9
-3
3
The absolute value is the distance from a given number to 0. In our example, we are given -3. This number is 3 units away from 0, and thus the absolute value of -3 is 3.
If a number is negative, its absolute value will be the positive number with the same magnitude. If a number is positive, it will be its own absolute value.
Example Question #13 : Algebra Ii
Notice that the equation 

Since the absolute value expression will always produce a positive number and the right side of the equation is negative, a negative number must be added to the result of the absolute value expression to satisfy the equation. Therefore the term outside of the absolute value expression (in this case 

Since 


Simplifying and solving this equation for 
Example Question #14 : Algebra Ii
What are the possible values for 
The absolute value measures the distance from zero to the given point.
In this case, since 


Example Question #4 : Absolute Value
Example Question #11 : Algebra Ii
Solve:
No solution
All real numbers
The absolute value can never be negative, so the equation is ONLY valid at zero.
The equation to solve becomes 
Example Question #1 : Absolute Value
Solve for 
To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.

and
This gives us:

However, this question has an 




Our final solution is then
Example Question #11 : Mathematical Relationships And Basic Graphs
Solve for 
Divide both sides by 3.
Consider both the negative and positive values for the absolute value term.
Subtract 2 from both sides to solve both scenarios for 
Example Question #1 : Graphing Absolute Value
Find the 
To find the 

To solve absolute value equations, we must understand that the absoute value function makes a value positive. So when we are solving these problems, we must consider two scenarios, one where the value is positive and one where the value is negative.
Now we must set up our two scenarios:

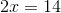

Certified Tutor
Certified Tutor
All High School Math Resources















































































