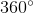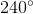How to find the angle of clock hands
Help Questions
Math › How to find the angle of clock hands
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
35°
55°
60°
65°
72°
Explanation
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
What is the measure, in degrees, of the acute angle formed by the hands of a 12-hour clock that reads exactly 3:10?
35°
55°
60°
65°
72°
Explanation
The entire clock measures 360°. As the clock is divided into 12 sections, the distance between each number is equivalent to 30° (360/12). The distance between the 2 and the 3 on the clock is 30°. One has to account, however, for the 10 minutes that have passed. 10 minutes is 1/6 of an hour so the hour hand has also moved 1/6 of the distance between the 3 and the 4, which adds 5° (1/6 of 30°). The total measure of the angle, therefore, is 35°.
If a clock reads 8:15 PM, what angle do the hands make?
Explanation
A clock is a circle, and a circle always contains 360 degrees. Since there are 60 minutes on a clock, each minute mark is 6 degrees.
The minute hand on the clock will point at 15 minutes, allowing us to calculate it's position on the circle.
Since there are 12 hours on the clock, each hour mark is 30 degrees.
We can calculate where the hour hand will be at 8:00.
However, the hour hand will actually be between the 8 and the 9, since we are looking at 8:15 rather than an absolute hour mark. 15 minutes is equal to one-fourth of an hour. Use the same equation to find the additional position of the hour hand.
We are looking for the angle between the two hands of the clock. The will be equal to the difference between the two angle measures.
It is 4 o’clock. What is the measure of the angle formed between the hour hand and the minute hand?
Explanation
At four o’clock the minute hand is on the 12 and the hour hand is on the 4. The angle formed is 4/12 of the total number of degrees in a circle, 360.
4/12 * 360 = 120 degrees
It is 4 o’clock. What is the measure of the angle formed between the hour hand and the minute hand?
Explanation
At four o’clock the minute hand is on the 12 and the hour hand is on the 4. The angle formed is 4/12 of the total number of degrees in a circle, 360.
4/12 * 360 = 120 degrees
The clock in the classroom reads 5:00pm. What is the angle that the hands are forming?
Explanation
Since the clock is a circle, you can determine that the total number of degrees inside the circle is 360. Since a clock has 12 numbers, we can divide 360 by 12 to see what the angle is between two numbers that are right next to each other. Thus, we can see that the angle between two numbers right next to each other is 

Find the angle between the minute and hour hand at 8:20 PM.
Explanation
The distance between each notch on the clock is 6 degrees because there are 360 degrees on the clock, and there are 60 notches total. The minute hand is at notch #20, and so it is 120 degrees from the top. The hour hand is a little past notch #40 because the time is a little past hour 8. Thus, the hour hand is a little past 240 degrees from the top, going clockwise (
In each hour, the hour hand goes 5 notches, or 30 degrees. Because it is now 20 minutes past the hour, a third of an hour has passed. One third of 30 degrees is 10 degrees. Thus, the hour hand is 10 degrees past notch #40. The hour hand is 250 degrees from the top, going clockwise. The angle between the two hands is thus 130 degrees.
A clock currently reads 2:00. What is the size of the angle formed between the hour and minute hands?
Explanation
The interior angle of a sector is equal the the angle of the sector. If the entire circumference was the sector, it would equal 


Cross multiply and solve for 
The time on a clock reads 5:00. What is the measure of the central angle formed by the hands of the clock?
Explanation
First, remember that the number of degrees in a circle is 360. Then, figure out how many degrees are in between each number on the face of the clock. Since there are 12 numbers, there are 
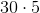

When making a pie chart, how many degrees should be allotted for 
Explanation
This is a proportion problem