All High School Math Resources
Example Questions
Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar
Are the triangles similar? If so, solve for 

The triangles are not similar
Yes;
Yes;
Yes;
Yes;
The triangles are similar because of the side-angle-side postulate.
Side:
Angle:
Side:
The third side must also have a 2:3 ratio.
Cross-multiply, and solve for 
Example Question #2 : How To Find If Two Acute / Obtuse Triangles Are Similar
Are the triangles similar? If so, solve for 
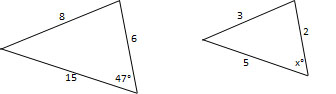
Yes;
Yes;
Yes;
The triangles are not similar
The triangles are not similar
The triangles are not similar, as proven by the side-side-side postulate.
The third side does not follow the same ratio of the other two, thus the triangles are not similar.
Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar


The perimeter is equal to the sum of the three sides. In similar triangles, each side is in proportion to its correlating side. The perimeters are also in equal proportion.
Perimeter A = 45” and perimeter B = 135”
The proportion of Perimeter A to Perimeter B is 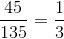
This applies to the sides of the triangle. Therefore to get the any side of Triangle B, just multiply the correlating side by 3.
15” x 3 = 45”
10” x 3 = 30“

Example Question #51 : Acute / Obtuse Triangles
Side-Side-Side Postulate
Side-Side-Angle Postulate
Side-Angle-Side Postulate
Angle-Angle Postulate
Angle-Angle Postulate
Angle-Angle Postulate: if two angles of one triangle are equal to two corresponding angles of another triangle, the triangles must be similar.
In this example, the triangles share one angle, which must be equal. Additionally, the triangles contain segments that are parallel to each other. When two parallel lines are crossed by another line, the corresponding angles must be equal. Each angle in one triangle is congruent with its corresponding angle in the other triangle, indicating that they are similar.
Example Question #1 : How To Find If Two Acute / Obtuse Triangles Are Similar
Side-Side-Side Postulate
Side-Angle-Side Postulate
Angle-Angle Postulate
Side-Side-Angle Postulate
Side-Angle-Side Postulate
The Side-Angle-Side Postulate considers two corresponding sides and the included angle. The included angles must be congruent, and the ratios of the two corresponding sides must be equal. If both criteria are satisfied, then the triangles are similar.
In this problem, there is a shared angle, making it equal for the two triangles. Now, consider the ratios of the sides.
Simplify the fractions.
because the ratios are equal, the triangles are similar by the Side-Angle-Side postulate.
Example Question #52 : Acute / Obtuse Triangles
The ratio of the side lengths of a triangle is 7:10:11. In a similar triangle, the middle side is 9 inches long. What is the length of the longest side of the second triangle?
7.7
12.1
9
10
9.9
9.9
Side lengths of similar triangles can be expressed in proportions. Establish a proportion comparing the middle and long sides of your triangles.
10/11 = 9/x
Cross multiply and solve for x.
10x = 99
x = 9.9
Example Question #53 : Acute / Obtuse Triangles
Two triangles are similar to each other. The bigger one has side lengths of 12, 3, and 14.
The smaller triangle's shortest side is 1 unit in length. What is the length of the smaller triangle's longest side?
Because the triangles are similar, a ratio can be set up between the triangles' longest sides and shortest sides as such: 14/3 = x/1. Solving for x, we obtain that the shortest side of the triangle is 14/3 units long.
Example Question #2 : How To Find If Two Acute / Obtuse Triangles Are Similar
A triangle with two equal angles is called a(n) __________.
equilateral triangle
disjoint triangle
Pythagoras triangle
isosceles triangle
right triangle
isosceles triangle
An isoceles triangle is a triangle that has at least two congruent sides (and therefore, at least two congruent angles as well).
All High School Math Resources

































