All GRE Math Resources
Example Questions
Example Question #3 : Geometry
What is the area of a circle, one-quarter of the circumference of which is 5.5 inches?
π/3
121π
225π
121/π
121/π
Here, you need to “solve backward” from the data you have been given. We know that 0.25C = 5.5; therefore, C = 22. In order to solve for the area, we will need the radius of the circle. This can be obtained by recalling that C = 2πr. Replacing 22 for C, we get 22 = 2πr.
Solve for r: r = 22 / 2π = 11 / π.
Now, we solve for the area: A = πr2. Replacing 11 / π for r: A = π (11 / π)2 = (121π) / (π2) = 121 / π.
Example Question #1 : Circles
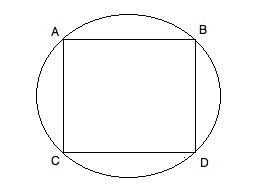
In the diagram above, square ABCD is inscribed in the circle. If the area of the square is 9, what is the area of the circle?
9π
3√(2)π
3π
18π
4.5π
4.5π
If the area of the square is 9, then s2 = 9 and s = 3. If the sides thus equal 3, we can calculate the diagonals (either CB or AD) by using the 45-45-90 triangle ratio. For a side of 3, the diagonal will be 3√(2). Note that since the square is inscribed in the circle, this diagonal is also the diameter of the circle. If it is such, the radius is one half of that or 1.5√(2).
Based on that value, we can computer the circle’s area:
A = πr2 = π(1.5√(2))2 = (2.25 * 2)π = 4.5π
Example Question #2 : Geometry
Quantitative Comparison
Quantity A: Area of a circle with radius r
Quantity B: Perimeter of a circle with radius r
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined from the information given.
Try different values for the radius to see if a pattern emerges. The formulas needed are Area = πr2 and Perimeter = 2πr.
If r = 1, then the Area = π and the Perimeter = 2π, so the perimeter is larger.
If r = 4, then the area = 16π and the perimeter = 8π, so the area is larger.
Therefore the relationship cannot be determined from the information given.
Example Question #1 : How To Find The Area Of A Circle
Quantitative Comparison
A circle has a radius of 2.
Quantity A: The area of the circle
Quantity B: The circumference of the circle
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The relationship cannot be determined from the information given.
The two quantities are equal.
This is one of the only special cases where the area equals the circumference of the circle. The Area = πr2 = 4π. The circumference = 2πr = 4π.
Note: For a quantitative comparison such as this one where the columns have numeric values instead of variables, the answer will rarely be "cannot be determined".
Example Question #11 : Circles
Quantitative Comparison
Quantity A: Area of a right triangle with sides 7, 24, 25
Quantity B: Area of a circle with radius 5
Quantity A is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.
Quantity B is greater.
Quantity A is greater.
Quantity A: area = base * height / 2 = 7 * 24/2 = 84
Quantity B: area = πr2 = 25π
Now we have to remember what π is. Using π = 3, the area is approximately 75. Using π = 3.14, the area increases a little bit, but no matter how exact an approximation for π, this area will never be larger than Quantity A.
Example Question #11 : Geometry
If a circular garden with a radius of 3 ft. is bordered by a circular sidewalk that is 2 ft. wide, what is the area of the sidewalk?
To solve this problem, you must find the area of the entire circle (garden and sidewalk) and subtract it by the area of the inner garden. The entire area has a radius of 5 ft. (3 ft. radius of the garden plus the 2 ft. wide sidewalk), giving it an area of 


Example Question #11 : Geometry
If a circular monument with a radius of 30 feet is surrounded by a circular garden that is 20 feet wide, what is the area of the garden?
To find the area of the garden, you need to find the entire area and subtract that by the area of the inner circle, or the monument. The radius of the larger circle is 50, which makes its area 


Example Question #11 : Circles
A small circle with radius 5 lies inside a larger circle with radius x. What is the area of the region inside the larger circle, but outside of the smaller circle, in terms of x?
Since the answers are in terms of pi, simply find the area of each circle in terms of x and ∏:
Smaller: ∏(5)2 = 25∏
Larger: ∏x2
We must subtract the inner circle from the outer circle; this translates to ∏x2-25∏.
Example Question #12 : Geometry
Given circle O with a diameter of 2 and square ABCD inscribed within circle O, what is the area of the shaded region?

2
4
4π – 2
π – 2
π – 2
There are two steps to this problem: determining the area of the circle and determining the area of the square. The area of the circle is πr2 which is π(2/1)2 or π. AD is a diameter of circle O and creates two isosceles right triangles with ACD and ABD. The relationship between sides of an isosceles right triangle is 1 : 1 : √2. Thus the sides of square ABCD are √2 and the area is 2. The area of the shaded region is the area of the circle minus the area of the square, or π – 2.
Example Question #11 : Geometry
For 


Cannot be determined.
two
The two values are equal.
Therefore the 16 inch pizza is the better deal.
All GRE Math Resources