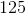All GRE Math Resources
Example Questions
Example Question #31 : Geometry
What is the perimeter of a pie piece if the pie is sliced into 40 degree pieces and its area is 361π?
38π
40.1π
38 + 38π/9
2.1
38π/9
38 + 38π/9
The perimeter of a given pie-piece will be equal to 2 radii plus the outer arc (which is a percentage of the circumference). For our piece, this arc will be 40/360 or 1/9 of the circumference. If the area is 361π, this means πr2 = 361 and that the radius is 19. The total circumference is therefore 2 * 19 * π or 38π.
The total perimeter of the pie piece is therefore 2 * r + (1 / 9) * c = 2 * 19 + (1/9) * 38π = 38 + 38π/9
Example Question #1 : Sectors
What is the length of the arc of a circle with radius 10 that traces a 50 degree angle?
25π
25π/9
25π/29
20π/9
25π/7
25π/9
length of an arc = (degrees * 2πr)/360 = (50 * 2π * 10)/360 = 25π/9
Example Question #3 : Sectors
An ant walks around the edge of circular pizzas left on the counter of a pizza shop. On most days, it is shaken off the pizza before it manages to walk the complete distance.
Quantity A: The distance covered by the ant when walking over four slices of a pizza with a diameter of 

Quantity B: The distance covered by the ant when walking over a complete personal pizza with a diameter of 
What can we say about the two quantities?
Quantity B is larger.
Quantity A is larger.
The two quantities are equal.
The relationship between the two quantities cannot be determined.
Quantity B is larger.
Let's compute each quantity.
Quantity A
This is a little bit more difficult than quantity B. It requires us to compute an arc length, for the ant does not walk around the whole pizza; however, this is not very hard. What we know is that the ant walks around 

Now, we know the circumference of a circle is 
For our example, let's use the latter. Since 
However, our ant walks around only part of this, namely:
Quantity B
This is really just a matter of computing the circumference of the circle. For our value, we know this to be:
Now, we can compare these by taking quantity A and reducing the fraction to be 
Example Question #33 : Plane Geometry
A circle of radius 




The formula for an arc length, 


Note that 
Conversely, for a known arc length and unknown angle, this equation can be rewritten as follows:
Plugging in the given values, it is therefore possible to find the missing angle:
Example Question #2 : Sectors
Find the radius of the given circle:

The answer cannot be determined from the information given.
To solve this problem, realize that an inscribed angle (an angle formed by two chords) is equal to twice the central angle formed by connecting the origin to the inscribed angle's endpoints:

Now, the formula for an arc length, 


Since the radius is the unknown, this equation can be rewritten as:
Plugging in our values, we find:
Example Question #3 : Sectors
A given pizza with a 


To solve this, notice that one piece of pizza comprises 



Rounding, this is 
Example Question #31 : Geometry
An ant begins at the center of a pie with a 12" radius. Walking out to the edge of pie, it then proceeds along the outer edge for a certain distance. At a certain point, it turns back toward the center of the pie and returns to the center point. Its whole trek was 55.3 inches. What is the approximate size of the angle through which it traveled?
74.76°
128.21°
91.44°
81.53°
149.52°
149.52°
To solve this, we must ascertain the following:
1) The arc length through which the ant traveled.
2) The percentage of the total circumference in light of that arc length.
3) The percentage of 360° proportionate to that arc percentage.
To begin, let's note that the ant travelled 12 + 12 + x inches, where x is the outer arc distance. (It traveled the radius twice, remember); therefore, we know that 24 + x = 55.3 or x = 31.3.
Now, the total circumference of the circle is 2πr or 24π. The arc is 31.3/24π percent of the total circumference; therefore, the percentage of the angle is 360 * 31.3/24π. Since the answers are approximations, use 3.14 for π. This would be 149.52°.
Example Question #32 : Geometry
A study was conducted to determine the effectiveness of a vaccine for the common cold (Rhinovirus sp.). 1000 patients were studied. Of those, 500 received the vaccine and 500 did not. The patients were then exposed to the Rhinovirus and the results were tabulated.

Table 1 shows the number of vaccinated and unvaccinated patients in each age group who caught the cold.
Suppose the scientists wish to create a pie chart reflecting a patient's odds of catching the virus depending on vaccination status and age group.
All 1000 patients are included in this pie chart.
What would be the angle of the arc for the portion of the chart representing vaccinated patients of all age groups who caught the virus?
18°
10°
Insufficient information to answer this question
36°
60°
18°
First, we must determine what proportion of the 1000 patients were vaccinated and caught the virus. The total number of patients who were vaccinated and caught the virus is 50.
18 + 4 + 5 + 4 + 19 = 50
The proportion of the patients is represented by dividing this group by the total number of participants in the study.
50/1000 = 0.05
Next, we need to figure out how that proportion translates into a proportion of a pie chart. There are 360° in a pie chart. Multiply 360° by our proportion to reach the solution.
360° * 0.05 = 18°
The angle of the arc representing vaccinated patients who caught the virus is 18°.
Example Question #31 : Circles
A group of students ate an 



You will not need all of the information given in the prompt in order to answer this question successfully. You really only need to know that there were 



Example Question #31 : Geometry
If the outer arc of 1/12th of a circular pie is 7π, what is the area of 1/4th of the pie?
21π
None of the other answers
10.5π
441π
1764π
441π
Our initial data tells us that (1/12)c = 7π or (1/12)πd = 7π. This simplifies to (1/12)d = 7 or d = 84. Furthermore, we know that r is 42. Given this, we can ascertain the area of a quarter of the whole pie by taking one fourth of the whole area or 0.25 * π * 422 = 0.25 * 1764 * π = 441π
All GRE Math Resources