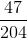Conditional Probability
Help Questions
Finite Mathematics › Conditional Probability
Jack and Jill agree to a game, the rules of which are as follows:
A card will be drawn from a standard 53-card deck (including the joker). If a club is drawn, Jack will pay Jill $100. If a card of any other suit is drawn, Jill will pay Jack $20.
For the game to be fair, what must happen in the event the joker is drawn?
(Note: The joker is not considered to be of any of the four suits.)
Jill must agree to pay Jack $520.
Jack must agree to pay Jill $520.
There should be no payment either way.
Jill must agree to pay Jack $780.
Jack must agree to pay Jill $780.
Explanation
We will consider the value of each event to Jill; positive values refer to Jack paying Jill, and negative values refer to Jill paying Jack.
There are 53 equiprobable outcomes. Along with their probabilities and their values to Jill, they are:

The value to Jill, 

Since Jill wins $100 in this event, the value to her is

Since Jill loses $20, the value to her is

The expected value 
The game is to be fair, meaning that 
Solve for
Jill must agree to pay Jack $520 in the event of the draw of the joker.
A card is drawn at random from a standard deck of 52 cards (the joker is not included), and its rank and suit are recorded.
Which of the following changes both the probability of drawing a black card and that of drawing an ace?
-
Replacing the ace of spades with the joker
-
Adding the joker
-
Removing the ace of spades
(1), (2), and (3)
(1) and (2) only
(1) and (3) only
(2) and (3) only
(1) only
Explanation
If a card is drawn at random from a standard deck of 52, the probability of drawing one of the 26 black cards is 

(1) If the ace of spades is replaced with the joker, this leaves 25 black cards and 3 aces out of a total of 52 cards. The probability of drawing one of the 25 black cards is 

(2) If the joker is added, there are still 26 black cards and 4 aces, but the deck now has 53 cards. The probability of drawing one of the 25 black cards is 

(3) If the ace of spades is removed, this leaves 25 black cards and 3 aces out of a total of 51 cards. The probability of drawing one of the 25 black cards is 

In all three cases, both probabilities have changed.
Jack and Jill agree to a game. A card is drawn at random from a standard deck of 52. If the card is a spade, Jack plays Jill $75. If the card is anything else, Jill pays Jack $25.
True or false: This is an example of a fair game.
True
Fallse
Explanation
The fairness or unfairness of the game is a function of the expected value, which can be calculated by multiplying the probability of each outcome by its value, and adding the products.
We will examine the value of the game to Jack; a positive value indicates a gain to Jack, and a negative value indicates a gain to Jill.
Since only suits matter in this game, there are four equiprobable outcomes. One is favorable to Jill, and the other three are favorable to Jack. There are two events, a win for Jill and a win for Jack, which we will call 


Probability:
Value to Jack:

Probability:
Value to Jack:
The expected value of one play of the game to Jack is
The game is fair.
The odds in favor of an event occurring are 17 to 4. To the nearest hundredth, what is the probability of the event happening?
Explanation
If the odds in favor of an event are 





Jack and Jill agree to a game. A card is drawn at random from a standard deck of 52 (no joker). If the card is a face card (king, jack, queen) or a ten, Jack plays Jill $50. If the card is anything else, Jill pays Jack $25.
Which of the following is true of the game?
The value of the game is $1.92 in Jack's favor.
The game is fair.
The value of the game is $1.92 in Jill's favor.
The value of the game is $7.69 in Jill's favor.
The value of the game is $7.69 in Jack's favor.
Explanation
The fairness or unfairness of the game is a function of the expected value, which can be calculated by multiplying the probability of each outcome by its value, and adding the products.
We will examine the value of the game to Jack; a positive value indicates a gain to Jack, and a negative value indicates a gain to Jill.
Since only ranks matter in this game, there are thirteen equiprobable outcomes. Four are favorable to Jill, and the other nine are favorable to Jack. There are two events, a win for Jill and a win for Jack, which we will call 


Probability:
Value to Jack:

Probability:
Value to Jack:
The expected value of one play of the game to Jack is

From a standard deck of 52 cards (the joker is not included) a card is drawn. The person who draws it reveals only that the card is black.
A second card is drawn without replacement. What is the probability that the card will be a spade?
Explanation
This is a conditional probability problem.
There are thirteen spades and thirteen clubs; since the first card is known to be black, the probability of the first card being a spade (or club) is

The probability of the second card being a spade depends on the suit of the first card. The probability of the second card being a spade, given that the first card was also a spade, is
The probability of the second card being a spade, given that the first card was a club, is
The overall probability that the second card will be a spade is
The twelve face cards (kings, queens, jacks) are separated from a standard deck of 52 cards. Two cards are selected at random from the twelve, without replacement. What is the probability that both cards will be kings?
Explanation
Two cards are drawn from the deck without regard to order, so the sample space 
The event 
The probability of the event is
The probability of an event is 
17 to 8
25 to 17
25 to 8
42 to 25
42 to 17
Explanation
The odds in favor of an event are equal to the ratio of the probability of the event to that of the opposite event. Therefore, we want to determine 

or 17 to 8 in favor.







![\$ 53(0)=53 \left [\frac{1}{53} A(J)+ \frac{13}{53} ($ 100)+ \frac{39}{53} (-$20) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1048918/gif.latex)