All Common Core: High School - Statistics and Probability Resources
Example Questions
Example Question #311 : High School: Statistics & Probability
A cat will chase a laser pointer with probability .39. Given that the cat is chasing the laser, a dog will chase the laser with probability .73. What is the probability that both the dog and cat chase the laser pointer?
1.12
.39
.34
.28
.73
.28
Example Question #2 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate 
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, uniformity in probability models and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.
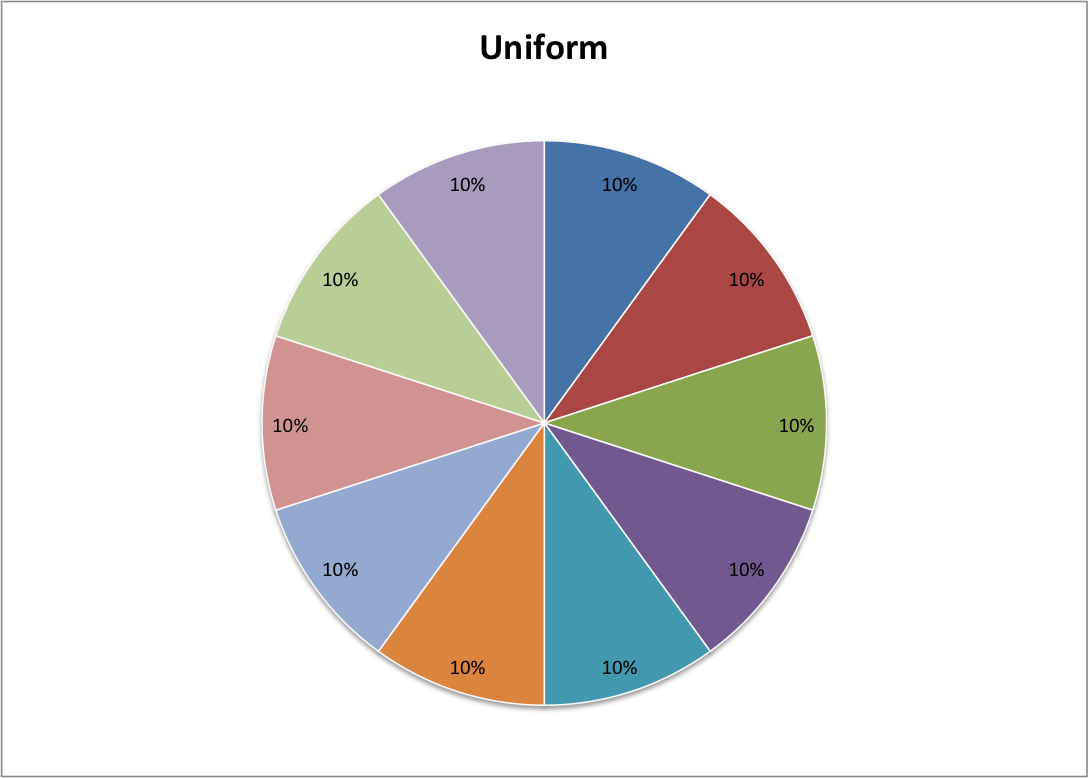
On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication rule of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #1 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #2 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate 
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #5 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #6 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #7 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #8 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #9 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
Example Question #10 : General Multiplication Rule In A Uniform Probability Model: Ccss.Math.Content.Hss Cp.B.8
Use the general multiplication rule to solve for the given probability model. For events A and B, calculate P(A\cap B) given the following information:
Cannot be determined
In order to solve this problem, we need to discuss probabilities, conditional probabilities, and the general multiplication rule of probability. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
Probabilities expressed in fraction form will have values between zero and one. One indicates that an event will definitely occur, while zero indicates that an event will not occur. Likewise, probabilities expressed as percentages possess values between zero and one hundred percent where probabilities closer to zero are unlikely to occur and those close to one hundred percent are more likely to occur.
Now that we understand the definition of a probability in its most general sense, we can investigate conditional probabilities. A conditional probability is defined as the probability that event B will occur given the information that an event A has already occurred.

It is expressed using the following equation:
In this equation, the probability of event B given that event A has occurred is equal to the probability of the intersection of events A and B divided by the probability of event A. It is important to note that if the events are independent, then the probability of event B given event A is simply the probability of event B because event A does not affect it.
Before we can use this information to discuss the general multiplication rule of probability, we must understand what is meant by the terms uniform and non-uniform in a probability model. In a uniform probability mode all events possess an equal chance of occurring. For instance, rolling any one side on a six sided fair die will have the same probability: one out of six. Likewise, the probability of a spinner landing on any of the colored spaces in the uniform figure is ten percent; therefore, uniform probability models posses events that all have the same probability of occurring.

On the other hand, in non-uniform models events do not share an equal probabilities. For instance, someone may weight or alter a die in order to increase the chances of rolling a particular number. Likewise, the probability of a spinner landing on each of the colored spaces in the non-uniform image possess differing probabilities; thus, the probabilities of non-uniform events differ from one another.

Now that we understand what is meant by uniform and non-uniform probability models, we can discuss the general multiplication role of probability. First, it can only be used to answer questions regarding uniform models because non-uniform models require more advanced mathematics. Second, the formula is based upon the conditional probability formula. Let's start by reviewing this formula.
Let's begin by multiplying each side of the equation by the following probability:
Cross out like terms and simplify in order to create our first rule of general multiplication of probabilities.
Next, we can use the same model to create another multiplication formula for the conditional probability:
Simplify as before in order to create our second rule of general multiplication of probabilities.
We can create a third rule of general multiplication of probabilities by setting the two equations equal to one another by using the like term:
These formulas enable us to easily solve probabilities problems that may be lacking information. Let's use this information to solve the problem. We need to find the probability of 
We will start by choosing the correct formula. In this case, we shall use the first formula:
Now, we can substitute in known values.
Solve.
All Common Core: High School - Statistics and Probability Resources



























































































