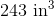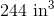Finding Volume of a Rectangular Prism
Help Questions
7th Grade Math › Finding Volume of a Rectangular Prism

The above diagram shows a rectangular solid. The shaded side is a square. In terms of 
Explanation
A square has four sides of equal length, as seen in the diagram below.

The volume of the solid is equal to the product of its length, width, and height, as follows:

Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
A rectangular prism has the following dimensions:
Length:
Width:
Height:
Find the volume.
Explanation
Given that the dimensions are: 






This final value can be approximated to 
Solve for the volume of a prism that is 4m by 3m by 8m.
Explanation
The volume of the rectangle
so we plug in our values and obtain

The dimensions of Treasure Chest A are 39” x 18”. The dimensions of Treasure Chest B are 16” x 45”. Both are 11” high. Which of the following statements is correct?
Treasure Chest A and B can hold the same amount of treasure.
Treasure Chest A can hold more treasure.
Treasure Chest B can hold more treasure.
Treasure Chest A has the same surface area as Treasure Chest B.
There is insufficient data to make a comparison between Treasure Chest A and Treasure Chest B.
Explanation
The volume of B is 7920 in3. The volume of A is 7722 in3. Treasure Chest B can hold more treasure.
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
Explanation
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. Find the volume of the prism.
Find the volume of a rectangular prism via the following:
Where l, w, and h are the length width and height, respectively.
We know our length and width, and we are told that our height is triple the length, so...
Now that we have all our measurements, plug them in and solve:
Calculate the volume of the provided figure.

Explanation
In order to solve this problem, we need to recall the volume formula for a rectangular prism:
Now that we have the correct formula, we can substitute in our known values and solve:
An aquarium is shaped like a perfect cube; the perimeter of each glass face is 

Note:
Insufficient information is given to answer the question.
Explanation
A perfect cube has square faces; if a face has perimeter 


Its capacity in liters is 


This rounds to