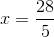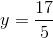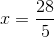All College Algebra Resources
Example Questions
Example Question #1 : Augmented Matrices
Solve the following Augmented Matrix.
First step is to multiply Row 1 by 
Now we have two equations.

Solve for y first, and then plug the result into the other equation.
Example Question #2 : Augmented Matrices
Write the augmented matrix for the system of equations given below and perform row operations until the augmented matrix is in row reduced echelon form, then read off the solution.
Note that interchanging rows in a matrix does not change the solution so check for interchanged rows if you don't see your augmented matrix among the augmented multiple choices.
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
Augmented Matrix of the System
Row Reduced Echelon Form
Solutions:
1) Rewrite both the equations to tidy up and make sure all constant terms are isolated on one side of the equation. This will make it easier to write the augmented matrix.
2) Write the augmented matrix corresponding to the system.
Quick Refresher:
The identity matrix 
We want to perform row operations until we have reduced the augmented matrix down to the form,
where the column vector 


3) Now we can perform a succession of row operations to reduce to the desired form,
We can start by cancelling out the 
Now we need a 


Now we need a 


Now we need a 

4) Write the Solution Set:
Example Question #2 : Augmented Matrices
Solve for x, y, and z.
From the augmented matrix, we see that
Now perform row operations to find x and y.
1. Switch Row 1 with Row 2:
2. Multiply Row 1 by-2 and add it to Row 2:
3. Multiply Row 3 by 13 and multiply Row 2 by -1. Add the two rows for a new Row 2:
4. Multiply Row 3 by -5 and add it to Row 1. Multiply Row 2 by -2 and add it to Row 1:
Example Question #2 : Augmented Matrices
Suppose you are trying to solve a system of two linear equations in two variables using the Gauss-Jordan elimination method on an augmented matrix. After a row operation, the matrix that appears is

How many solutions does the system have?
None
One
Infinitely many
Infinitely many
If, during the process of Gauss-Jordan elimination, any row becomes an all zero-row, it ceases to be a factor in determining the solution set. We must examine the top row of the matrix alone.
Remember that each entry to the left of the divider represents a coefficient and each entry to the right represents a constant. Therefore, the top row in the matrix

represents the equation

or, equivalently,
Therefore, 

Example Question #3 : Augmented Matrices
Suppose you are trying to solve a system of two linear equations in two variables using the Gauss-Jordan elimination method on an augmented matrix. After a row operation, the matrix that appears is

How many solutions does the system have?
One
None
Infinitely many
One
When applying the Gauss-Jordan method to solve a two-by-two linear system, the objective is to use row operations to form an augmented matrix of the form


If this happens, then there is one and only one solution to the system, represented by the ordered pair 

is in this form, and there is one solution, 
Example Question #4 : Augmented Matrices
Suppose you are trying to solve a system of three linear equations in three variables using the Gauss-Jordan elimination method on an augmented matrix. After a row operation, the matrix that appears is

How many solutions does the system have?
None
One
Infinitely many
None
The red flag in this augmented matrix is the bottom row, which has 0's as all of its entries to the left of the divider and a nonzero entry to the right. Any time this happens during the process of Gauss-Jordan elimination, this signals that the system of equations has no solution.
Example Question #533 : College Algebra
Suppose you are trying to solve a system of three linear equations in three variables using the Gauss-Jordan elimination method on an augmented matrix. After a row operation, the matrix that appears is

How many solutions does the system have?
One
None
Infinitely many
Infinitely many
If, during the process of Gauss-Jordan elimination, any row becomes an all zero-row, it ceases to be a factor in determining the solution set. We must examine the other rows of the matrix.
Remember that each entry to the left of the divider represents a coefficient and each entry to the right represents a constant. Therefore, the two nonzero rows in the matrix

represent the equations
and

respectively.
The equations can be solved for 


and
Therefore, 



Example Question #31 : Systems Of Equations
When solving a system of three linear equations in three variables using the Gauss-Jordan elimination method, your initial augmented matrix is as follows:

Which of the following is notation for the next step you should perform?
When applying the Gauss-Jordan method to solve a three-by-three linear system, the objective is to use row operations to form an augmented matrix of the form


with 
Once the initial augmented matrix

is set up, the first step should always be to get a 1 in the upper left position; this is usually done by multiplying every element in Row 1 by the reciprocal of the first element in that row. Since the element in that position is 


Example Question #5 : Augmented Matrices
Use augmented matrices to solve the following system of equations:
Begin by constructing an augmented matrix for our system of equations:
Switch rows 1 and 2:

Add row 2 and twice row 1, to row 1:


Divide row 1 by 5:


Subtract 3 times row 1, from row 2:


Divide row 2 by 2:


Solution:
Plug the respective values of x and y into both equations to verify the solution:
Example Question #6 : Augmented Matrices
Use augmented matrices to solve the following system of equations:
Construct an augmented matrix for our system of equations:
Swap rows 1 and 3:


Subtract 2 times row 1 from row 2:


Subtract row 1 from row 3:


Add row 2 and three times row 3, to row 3:


Divide row 3 by 10:


Add row 3 to row 1:


Subtract row 3 from row 2:


Divide row 2 by 3:


Solution:
Plug the respective values of x, y, and z into all equations to verify the solution:
Certified Tutor
Certified Tutor
All College Algebra Resources