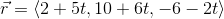Equations of Lines and Planes
Help Questions
AP Calculus BC › Equations of Lines and Planes
Write down the equation of the line in vector form that passes through the points 

Explanation
Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Determine the equation of the plane given by the following two vectors and the point 
Explanation
The equation of a plane is given by
where the normal vector is given by 
To find the normal vector to the plane, we must take the cross product of the two vectors.
We must write the determinant in order to take the cross product:
where i, j, and k are the unit vectors corresponding to the x, y, and z direction respectively.
Next, we take the cross product. One can do this by multiplying across from the top left to the lower right, and continuing downward, and then subtracting the terms multiplied from top right to the bottom left:
Now that we have the normal vector and a point on the plane, we plug everything into the equation:
which simplifies to
Find the approximate angle between the planes 

None of the other answers.
Explanation
Finding the angle between two planes requires us to find the angle between their normal vectors.
To obtain normal vectors, we simply take the coefficients in front of 
The (acute) angle between any two vector is

Substituting, we have

Determine the equation of the plane containing the three points
Explanation
The equation of a plane is defined as
where
is the normal vector of the plane.
To find the normal vector, we first get two vectors on the plane
and
and find their cross product.
The cross product is defined as the determinant of the matrix
Which is
Which tells us the normal vector is
Using the point
and the normal vector to find the equation of the plane yields
Simplified gives the equation of the plane
Find the unit tangent vector given by the curve
Explanation
To find the unit tangent vector for a given curve, we must find the derivative of each of the components of the curve, and then divide this vector - the tangent vector - by the magnitude of the tangent vector itself.
To start, let's find the derivatives:
We used the following rules to find them:


Next, we must find the magnitude of the tangent vector, by taking the square root of the sum of the squares the x, y, and z components. Note that the vector we were given was in unit vector notation, and i, j, and k are each equal to one unit, so they don't impact the magnitude of the vector (they simply indicate direction).
Finally, divide the tangent vector by its magnitude:
Find the unit tangent vector to the curve given by
Explanation
To find the unit tangent vector for a given curve, we must find the derivative of each of the components of the curve, and then divide this vector - the tangent vector - by the magnitude of the tangent vector itself.
To start, let's find the derivatives:
The derivatives were found using the following rules:

Next, we must find the magnitude of the tangent vector, by taking the square root of the sum of the squares the x, y, and z components. Note that the vector we were given was in unit vector notation, and i, j, and k are each equal to one unit, so they don't impact the magnitude of the vector (they simply indicate direction).
Finally, divide the vector by its magnitude:
Find the angle (in degrees) between the planes 
Explanation
A quick way to notice the answer is 
Typically though, to find the angle between two planes, we find the angle between their normal vectors.
A vector normal to the first plane is
A vector normal to the second plane is
Then using the formula for the angle between vectors, 

Find the equation of the plane that contains the point 

Explanation
Using the formula for a plane 



Find the equation of the plane that contains the point 
Explanation
To find the equation of a plane with a point 

Using the information from the problem statement, we get
Simplifying, we then get
Find the equation of the plane containing the points
Explanation
The equation of a plane is defined as
where 
To find the normal vector, we first get two vectors on the plane

and find their cross product.
The cross product is defined as the determinant of the matrix
Which is
Which tells us the normal vector is
Using the point 
Simplified gives the equation of the plane