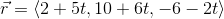All Calculus 3 Resources
Example Questions
Example Question #1 : Equations Of Lines And Planes
Write down the equation of the line in vector form that passes through the points 

Remember the general equation of a line in vector form:



Lets apply this to our problem.
Distribute the
Now we simply do vector addition to get
Example Question #2 : Equations Of Lines And Planes
Find the approximate angle between the planes 

None of the other answers.
Finding the angle between two planes requires us to find the angle between their normal vectors.
To obtain normal vectors, we simply take the coefficients in front of 
The (acute) angle between any two vector is

Substituting, we have

Example Question #3 : Equations Of Lines And Planes
Find the point of intersection of the plane 
The line and the plane are parallel.
Substituting the components of the line into those of the plane, we have
Substituting this value of 

Example Question #2 : 3 Dimensional Space
Find the angle (in degrees) between the planes 
A quick way to notice the answer is 
Typically though, to find the angle between two planes, we find the angle between their normal vectors.
A vector normal to the first plane is
A vector normal to the second plane is
Then using the formula for the angle between vectors, 

Example Question #4 : Equations Of Lines And Planes
Determine the equation of the plane that contains the following points.
The equation of a plane is defined as
where 
To find the normal vector, we first get two vectors on the plane

and find their cross product.
The cross product is defined as the determinant of the matrix
Which is
Which tells us the normal vector is
Using the point 
Simplified gives the equation of the plane
Example Question #2 : Equations Of Lines And Planes
Find the equation of the plane containing the points
The equation of a plane is defined as
where 
To find the normal vector, we first get two vectors on the plane

and find their cross product.
The cross product is defined as the determinant of the matrix
Which is
Which tells us the normal vector is
Using the point 
Simplified gives the equation of the plane
Example Question #5 : Equations Of Lines And Planes
Which of the following is an equation of a plane parallel to the plane 
None of the other answers
Planes that are parallel to each other only differ (if at all) by the constant on the right-hand side (when both sides are simplified). Since 

Example Question #3 : 3 Dimensional Space
Find a parametric representation of the curve of intersection of the cylinder 

We can begin by rewriting the expression for the cylinder as follows

This tells us that 


This gives us the representation of the curve of intersection as

Example Question #1 : Equations Of Lines And Planes
Find the equation of the plane containing the following points
The equation of a plane is defined as

where

is the normal vector of the plane.
To find the normal vector, we first get two vectors on the plane
and
and find their cross product.
The cross product is defined as the determinant of the matrix

Which is


Which tells us the normal vector is
Using the point
and the normal vector to find the equation of the plane yields

Simplified gives the equation of the plane
Example Question #10 : Equations Of Lines And Planes
Find the angle in degrees between the planes 
None of the other answers
To find the angle between the planes, we find the angle between their normal vectors.
We have


The angle between these two vectors is
All Calculus 3 Resources