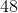All Basic Arithmetic Resources
Example Questions
Example Question #1 : Least Common Denominator
What is the least common denominator of the following fractions: 
The correct answer is 36. The best way to approach this problem is to take each denominator and list out its multiples. You can then find the common multiple between each denominator.
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42
Multiples of 12: 12, 24, 36, 48, 60
Multiples of 36: 36, 72, 108
Multiples of 18: 18, 36, 54, 72
From the above multiples, we can see that the least common denominator is 36.
Example Question #1 : Least Common Denominator
Find the least common denominator:
The least common denominator is the lowest number that has each denominator is a potential factor.
1. Multiply the two lowest denominators:
2. Check to see if the other denominators can factor into that denominator:
So 24 is your least common denominator. (48 is also a common denominator of all of these fractions, but it is not the lowest one)
Example Question #1 : Least Common Denominator
What is the least common denominator for the fractions 

To find the least common denominator, list out the multiples of both denominators until you find the smallest multiple that is shared by both.
4: 4, 8, 12, 16, 20, 24, 28, 32
7: 7, 14, 21, 28, 35
Because 28 is the first shared multiple of 4 and 7, it must be the least common denominator for these two fractions.
Example Question #2 : Least Common Denominator
For the fractions 

To find the least common denominator, list out the multiples of both denominators until you find the smallest multiple that is shared by both.
4: 4, 8, 12, 16, 20, 24
5: 5, 10, 15, 20, 25
Because 20 is the first shared multiple of 4 and 5, it must be the least common denominator for these two fractions.
Example Question #2 : Least Common Denominator
Find the least common denominator for the following fractions:
The least common denominator is the lowest common multiple of the denominators.
Multiple of 27: 27, 54, 81, 108, 135, 162, 189, 216, 243, 270
Multiple of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
Example Question #6 : Least Common Denominator
What is the least common denominator between the following fractions: 
The first step of finding the LCD of a set of fractions is to make sure each of the fractions are simplified. 



While simply multiplying all of the denominators will get you a common denominator between the fractions, it does not always give you the LCD.
Example Question #2 : Linear Equations With Fractions
What's the least common denominator between 

When finding the least common denominator, the quickest way is to multiply the numbers out.
In this case 


We can multiply them to get 
Another approach is to list out all the factors of each number and see which factor is in both sets first.
Notice 
Example Question #1 : Least Common Denominator
What's the least common denominator of 

When finding the least common denominator, the quickest way is to multiply the numbers out.
In this case 






Now, they don't share a common factor so basically multiply them out with the shared factor. Answer is 
Another approach is to list out the factors of both number and find the factor that appears in both sets first.
We can see that 
Example Question #3 : Least Common Denominator
What's the least common denominator of 

When finding the least common denominator, the quickest way is to multiply the numbers out. In this case 







Another approach is to list out the factors of each number. The factor that appears first in both set is the least common denominator.
We see that 
Example Question #2 : Least Common Denominator
What's the least common denominator among 


When finding the least common denominator, the quickest way is to multiply the numbers out. In the case of finding least common denominators among three or more numbers, it's critical there are no common factors between two of the denominators and of course all 3. This will ensure the answer will always be the least common denominator.
Say we just multiplied the numbers out. It's basically 










So this goes back to the statement: "In the case of finding least common denominators among three or more numbers, it's critical there are no common factors between two of the denominators and of course all 3." If I factored a 







All Basic Arithmetic Resources