Other Circular and Rotational Motion Concepts
Help Questions
AP Physics 1 › Other Circular and Rotational Motion Concepts

Michelle and her two brothers have some toys (spheres) they wish to roll down an incline in a race to the finish. Three objects are shown in which the siblings can choose from. Object A is a solid sphere with a mass of 





Object A only
Object C only
Object A & B will have the same outcome
Object B only
Explanation
This question deals with inertia. You can solve this mathematically, but the answer can also be found conceptually.
Inertia (in physics) is the object's ability to resist change in motion. In this case, it is based on mass, and how the mass of the object is distributed around it's rotational axis (Center of mass = middle of sphere). The larger the inertia, the more resistant to rotation; the more resistant to rotation, the slower the object will move down the incline.
Have you ever seen figure skating? When skaters want to make very tight turns or rotations, they pull their arms and head really close into their chest and crouch down into a smaller formation.
Why do skaters do this? Physics of course! The closer the mass of an object is to its COM, the smaller inertia they have, and the smaller resistance to change in motion. If the same skater (same height, weight, dimensions) attempts a turn in a further stretched out position (limbs untucked, etc), they will have a larger inertia, and therefore would not be able to turn as quickly as they could when tucked.
Okay so back to the spheres. As with the skaters, the further a mass is distributed from its COM, the larger the inertia. So between spheres A and B, which do you think has a lower inertia?
Sphere A has it's mass more evenly distributed throughout itself, whereas sphere B has the same mass, but with it's weight distributed solely to the exterior of its shell. Therefore, sphere A is a better choice that sphere B.
Now, what about sphere C? Typically, the larger the mass, the larger the inertia, same scenario for the objects' radii. The larger the M and R, the larger the inertia and the more resistant the object is to rotation. The best answer for Michelle to win is object A only. If you want to plug in some numbers to the inertia equations, I'll provide them here:
Laura plans on running track in college. She has a 5:08 mile time which means she can run 4 laps around a circular track (

Explanation
Displacement is the change in distance from start to finish
Where 
A track runner who weighs 750 N is running around a curve at a speed of 

Explanation
The equation for centripetal force on an object moving at a constant speed in a circular path is
The weight of the person is given to be 

We are given the velocity, 

Two cars are racing side by side on a circular race track. Which has the greater linear velocity?
The car on the outside
The car on the inside
They have the same linear velocity
Impossible to determine
Explanation
If the cars are racing side by side on a circular track, then they have the same angular velocity, because they complete their circles in the same amount of time. However, the car on the outside has a larger circle to complete, and thus must have a higher linear velocity.
Use energy conservation and your knowledge of rotational dynamics to solve the following problem
For a ball of radius 



Explanation
For this problem the ball picks up rotational velocity as well as linear velocity. Keeping this in mind we first set up our equation of conservation of energy
Because the object starts at rest the initial kinetic energy is 0 and likewise the final potential energy is 0 because it has spent all its potential energy to become kinetic.
Where m is mass of the ball, g is gravity, h is height of the ramp, v is final velocity of the ball, I is the moment of inertia of the ball, and w is the final rotational velocity of the ball.
Now because the ball is a solid sphere we can represent I and w as follows

Plugging this into our equation of energy conservation
Now solve for velocity:
Now plugging in our value for height, we arrive at a final answer of
Steve likes to work out after school. He goes to a new gym's free-weight section, he notices something strange about the dumbbells (see image).

What did Steve notice when he was doing his bicep curls?
It seemed harder than his usual 30lb workout
It seemed easier than his usual 30lb workout
It felt the same as his usual 30lb workout
He could not even lift the new dumbbell
Not enough information
Explanation
Inertia is the ability for an object to resist motion. In this case, inertia is determined by how far away the mass (weights) are distributed from the dumbbell's COM (center of handle). While there is no definitive equation for the "inertia of a dumbbell", we can conceptualize this. All inertia equations deal with a mass and a radius. The larger either of these numbers are, the larger the inertia! We know that the larger the inertia, the more resistant that object is to change in motion (or the more awkward it would be to pick up that object). With that said, it would be harder for Steve to pick up the new weight. Not because of the weight itself, but because of how that same weight is distributed around that object. Think about it this way; a piece of paper weighs roughly .16 oz. if I gave you a 1 cm cube that weighed .16 oz, which would be easier to pick up and balance on your head? I would most likely assume that you would say the cube. This is because the weight of the cube is more closely positioned near the COM, rather than the thin sheet of paper with it's weight evenly spread throughout 8.5" x 11".
Suppose that a mass hanging from a string attached to the ceiling is swinging in a circular motion, as shown in the diagram below.

If the mass is swinging at a constant speed of 

There is not enough information given
Explanation
To answer this question, we'll need to first identify all the forces acting on the hanging mass. To do this, we have to consider the forces acting along the y-axis and x-axis.
First, let's consider the forces in the y-direction. Since the mass is not moving in the y-direction, we know that the net force acting on the mass in the vertical direction is zero. We know that the weight of the mass acts downward, and the vertical component of the string's tension acts upward.
Next, let's look at the forces acting on the mass in the horizontal direction. Since the mass is moving in a uniform circular motion, we know that there is a centripetal force associated with this. Moreover, we know that the x-direction of the tension in the string is acting in the x-direction. Thus, this component of the string's tension must be providing the centripetal force.
Now, if we divide these two equations, we can cancel out the terms for tension and mass.
Further rearrangement of the above expression allows us to solve for the angle.
A wheel of radius 


Explanation
In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is 
Distance of one rotation equals: 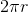
Since the wheel travels 
Distance of 
Suppose that an astronaut is traveling around the Earth at a constant speed. Which of the following statements regarding the astronaut's circular motion is correct?
The astronaut is constantly in a state of free-fall
The centripetal acceleration provided by the Earth's gravitational field is constant
If the astronaut's speed is doubled, his centripetal acceleration will also double
If the distance between the astronaut and the Earth were to double, the centripetal acceleration of the astronaut would also double
None of these
Explanation
For this question, we're asked to evaluate a true statement regarding circular motion. Hence, we'll need to look at each answer choice individually and consider whether it is true.
- The centripetal acceleration provided by the Earth's gravitational field is constant
This is not a true statement. Remember that acceleration is a vector. Even though the astronaut's centripetal acceleration is constant in magnitude, it is constantly changing direction as the force will always point towards the center of the Earth.
- If the astronaut's speed is doubled, his centripetal acceleration will also double
This statement is false. Remember the expression for centripetal force.
Hence, if the astronaut's speed becomes twice as great, then his acceleration will become four times as great.
- If the distance between the astronaut and the Earth were to double, the centripetal acceleration of the astronaut would also double
This statement is not true. Again, we need only look to the expression shown above for centripetal force to see why. Because the centripetal acceleration and distance are both inversely proportional to one another, doubling the distance of the astronaut from the Earth would cause the acceleration to become half as great. Thus, it would decrease, not increase.
- The astronaut is constantly in a state of free-fall
This is a true statement, and thus it is the correct answer. Objects that are orbiting the Earth experience a centripetal force due to gravity. If we picture a snapshot of the movement of the astronaut, he will be moving tangentially to his circular displacement. As the astronaut moves tangentially, the force of gravity serves as the centripetal force that "pulls" him back, such that the astronaut does not move down the tangential path. This continuous "pull" away from the tangential path at each instant essentially means that our astronaut will constantly fall towards the earth while maintaining his circular path, and is thus constantly in a state of free-fall, where he will be weightless.
A 55 cm rope is tied to the handle of a bucket, which is then spun in a vertical circle. The mass of the bucket is 3.3 kg. What is the minimum speed required such that the rope does not become slack when the bucket reaches the highest point in the circle?
Explanation
The faster that the object is moving while being spun, the greater the force of tension in the rope will be. Therefore, if we want to find the minimum speed of the bucket at the highest point in the circle such that the rope doesn't go slack, we should assume that the tension at that point is zero.
If the tension is zero, then the only force acting on the bucket at that point would be the force of gravity pulling down on the bucket. If the rope does not go slack, then the bucket must still be moving in a circular motion, so we can use the equation for circular/centripetal motion:
Since gravity is the only force, then
We can divide by 

The radius was given to us as 55 cm. We have to convert this to meters. Since