All Algebra II Resources
Example Questions
Example Question #2 : Applications
Twelve years ago, your grandma put money into a savings account for you that earns 

$10,778
$81,030
$21,170
$24,596
$8,103
$24,596
1. Use 




2. Solve for
You currently have $24,596 in your account.
Example Question #2 : Using E
Solve for
Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for x
Example Question #1 : Using E
Solve for
Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for
Example Question #1 : Using E
Solve for
Step 1: Achieve same bases

Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Example Question #5 : Using E
Solve for
Step 1: Achieve same bases
Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Example Question #2 : Using E
Solve for
Step 1: Achieve same bases
Step 2: Drop bases, set exponenets equal to eachother
Step 3: Solve for
Example Question #1 : Exponential And Logarithmic Functions
Solve:
The answer does not exist.
To solve 

Since 


The answer is:
Example Question #8 : Using E
Simplify:
In order to eliminate the natural log on both side, we will need to raise both sides as a power with a base of 
The equation will become:
Subtract 
Simplify both sides.
Divide both sides by negative five.
The answer is:
Example Question #9 : Using E
Simplify:
In order to cancel the natural logs, we will need to use 
The equation becomes:
Subtract 
The equation becomes:
Use the quadratic equation to solve for the possible roots.
Simplify the quadratic equation.
The answers are:
Example Question #10 : Using E
Simplify:
In order to get rid of the natural log, we will need to use the exponential term 
The equation becomes:
Subtract nine from both sides.
Divide by three on both sides.
Simplify both sides.
The answer is:
Certified Tutor
Certified Tutor
All Algebra II Resources









































































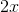
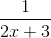























![2x-3 -[2x]+(3)=x^2-[2x]+(3)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/840260/gif.latex)



















