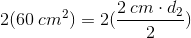How to find the length of the diagonal of a rhombus
Help Questions
Geometry › How to find the length of the diagonal of a rhombus
If the area of a rhombus is 

Explanation
The area of a rhombus is given below.
Substitute the given area and a diagonal. Solve for the other diagonal.
Assume quadrilateral 




Explanation
To find the value of diagonal 













The length of diagonal 

What is the second diagonal for the above rhombus?
Explanation
Because a rhombus has vertical and horizontal symmetry, it can be broken into four congruent triangles, each with a hypotenuse of 13 and a base of 5 (half the given diagonal).
The Pythagorean Theorem


The greater diagonal is twice the height of the triangles therefore, the greater diagonal becomes:
The area of a rhombus is 
Explanation
Let the shorter diagonal be 

Write the area of the rhombus.
Since we are solving for the shorter diagonal, it's best to setup the equation in terms 







Explanation
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Using the Pythagorean Theorem,
Assume quadrilateral 





Explanation
This problem relies on the knowledge of the equation for the area of a rhombus, 



Therefore, our final answer is that the diagonal





5
12
15
24
30
Explanation
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 



Because the diagonals bisect each other, we know:
Using the Pythagorean theorem,



Explanation
Using the Law of Sines,






Explanation
A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle 

Because the diagonals bisect each other, we know:
Using the Pythagorean Theorem,
Factoring,

The first solution is nonsensical for this problem.
If the area of a rhombus is 

Explanation
Write the formula for the area of a rhombus.
Plug in the given area and diagonal length. Solve for the other diagonal.