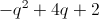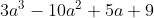All ACT Math Test Resources
Example Questions
Example Question #7 : Simplifying Polynomials
Simplify the following expression:
This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:

Combine these terms into one expression to find the answer:
Example Question #8 : Simplifying Polynomials
Simplify the following expression:
To simplify this expression you need to carefully remove the parentheses by distributing the negative sign across all terms in the second set of parentheses. To do this, just take the opposite of each of those signs. That gives you:
Then you can combine like terms:
Example Question #9 : Simplifying Polynomials
Choose the answer that best simplifies the following expression:
To solve this expression, you need to remove the parentheses, being careful to account for the negative prior to the second set of parentheses. To distribute that negative, take the opposite of each sign for that set of values. Then, combine like terms:
Example Question #10 : Simplifying Polynomials
Which of the following is equivalent to the expression 
A look at the answer choices tells you that you need to simplify the expression to arrive at fewer terms. To simplify this expression, you need to remove the parentheses and combine like terms. Fortunately, the process is to add the two parentheses and there are no coefficients or negatives between them, so you can simply lift the parentheses entirely and then combine. That leaves you with:
Example Question #1 : Triangle Similarity

In the figure above, lines DG, CF, and BE are parallel. If line segment AB = 6, line segment AE = 9, line segment EF = 10, and line segment FG = 11, what is the length of line AD?
21
23
22
24
20
20
A key to solving this problem comes in recognizing that you’re dealing with similar triangles. Because lines BE, CF, and DG are all parallel, that means that the top triangle ABE is similar to two larger triangles, ACF and ADG. You know that because they all share the same angle A, and then if the horizontal lines are all parallel then the bottom two angles of each triangle will be congruent as well. You’ve established similarity through Angle-Angle-Angle.
This means that the side ratios will be the same for each triangle. And for the top triangle, ABE, you know that the ratio of the left side (AB) to right side (AE) is 6 to 9, or a ratio of 2 to 3. Note then that the remainder of the given information provides you the length of the entire right-hand side, line AG, of larger triangle ADG. If AE is 9, EF is 10, and FG is 11, then side AG is 30. And since you know that the left-hand side has a 2:3 ratio to the right, then line segment AD must be 20.
Example Question #1 : Triangle Similarity
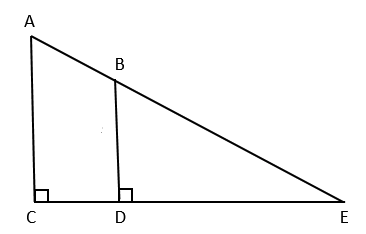
In the figure above, line segment AC is parallel to line segment BD. If line segment AC = 15, line segment BD = 10, and line segment CE = 30, what is the length of line segment CD?
15
25
20
10
5
10
This problem tests the concept of similar triangles. First, you should recognize that triangle ACE and triangle BDE are similar. You know this because they each have the same angle measures: they share the angle created at point E and they each have a 90-degree angle, so angle CAE must match angle DBE (the top left angle in each triangle.
Because these triangles are similar, their dimensions will be proportional. Since sides, AC and BD - which are proportional sides since they are both across from the same angle, E - share a 3:2 ratio you know that each side of the smaller triangle (BDE) will be 

Since the question asks for the length of CD, you can take side CE (30) and subtract DE (20) to get the correct answer, 10.
Example Question #1 : Triangle Similarity

In the figure above, line segments AD and BE intersect at point C. What is the length of line segment BE?
18
28
25
30
20
25
This problem hinges on your ability to recognize two important themes: one, that triangle ABC is a special right triangle, a 6-8-10 side ratio, allowing you to plug in 8 for side AB. And secondly, triangles ABC and CDE are similar triangles. You know this because each triangle is marked as a right triangle and angles ACB and ECD are vertical angles, meaning that they’re congruent. Since all angles in a triangle must sum to 180, if two angles are the same then the third has to be, too, so you’ve got similar triangles here.
With that knowledge, you know that triangle ECD follows a 3-4-5 ratio (the simplified version of 6-8-10), so if the side opposite angle C in ABC is 8 and in CDE is 12, then you know you have a 9-12-15 triangle. With the knowledge that side CE measures 15, you can add that to side BC which is 10, and you have the answer of 25.
Example Question #3 : Triangle Similarity

In the diagram above, line JX is parallel to line KY. If JX measures 16, KY measures 8, and the area of triangle JXZ is 80, what is the length of line segment XY?
6
4
8
3
5
5
An important point of recognition on this problem is that triangles JXZ and KYZ are similar. Each has a right angle and each shares the angle at point Z, so the third angles (XJZ and YKZ, each in the upper left corner of its triangle) must be the same, too.
Given that, if you know that JX measures 16 and KY measures 8, you know that each side of the larger triangle measures twice the length of its counterpart in the smaller triangle.
You also have enough information to solve for side XZ, since you’re given the area of triangle JXZ and a line, JX, that could serve as its height (remember, to use the 

Example Question #2 : Triangle Similarity

For the pictured triangles ABC and XYZ, which of the following is equal to the ratio 
The first important thing to note on this problem is that for each triangle, you’re given two angles: a right angle, and one other angle. Because all angles in a triangle must sum to 180 degrees, this means that you can solve for the missing angles.
In ABC, you have angles 36 and 90, meaning that to sum to 180 the missing angle ACB must be 54. And in XYZ, you have angles 90 and 54, meaning that the missing angle XZY must be 36.
Next, you can note that both triangles have the same angles: 36, 54, and 90. This means that the triangles are similar, which also means that their side ratios will be the same. You just need to make sure that you’re matching up sides based on the angles that they’re across from.
You’re given the ratio of AC to BC, which in triangle ABC is the ratio of the side opposite the right angle (AC) to the side opposite the 54-degree angle (BC). In triangle XYZ, those sides are XZ and XY, so the ratio you’re looking for is 
Example Question #2 : Triangle Similarity

In the figure above, triangle ABC is similar to triangle XYZ. If side XZ measures 10, what is the area of triangle XYZ?
48
28
40
32
24
24
Because the triangles are similar, you can tell that if the hypotenuse of the larger triangle is 15 and the hypotenuse of the smaller triangle is 10, then the sides have a ratio of 3:2 between the triangles. This allows you to fill in the sides of XYZ: side XY is 6 (which is 2/3 of its counterpart side AB which is 9) and since YZ is 8 (which is 2/3 of its counterpart side, BC, which is 12).
Since the area of a triangle is 

All ACT Math Test Resources