All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Given a right triangle with a leg length of 6 and a hypotenuse length of 10, find the length of the other leg, x.

4
8
16
64
8
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 62 = 102
Now we solve for x:
x2 + 36 = 100
x2 = 100 – 36
x2 = 64
x = 8
Also note that this is proportionally a 3/4/5 right triangle, which is very common. Always look out for a side-to-hypoteneuse ratio of 3/5 or 4/5, or a side-to-side ratio of 3/4, in any right triangle, so that you may solve such triangles rapidly.
Example Question #2 : How To Find The Length Of The Side Of A Right Triangle
In a right triangle a hypotenuse has a length of 8 and leg has a length of 7. What is the length of the third side to the nearest tenth?
Using the pythagorean theorem, 82=72+x2. Solving for x yields the square root of 15, which is 3.9
Example Question #3 : How To Find The Length Of The Side Of A Right Triangle
Given a right triangle with a leg length of 2 and a hypotenuse length of √8, find the length of the other leg, x.

2
10
6
√8
4
2
Using Pythagorean Theorem, we can solve for the length of leg x:
x2 + 22 = (√8)2 = 8
Now we solve for x:
x2 + 4 = 8
x2 = 8 – 4
x2 = 4
x = 2
Example Question #4 : How To Find The Length Of The Side Of A Right Triangle
The legs of a right triangle are 

Use the Pythagorean Theorem. The sum of both legs squared equals the hypotenuse squared.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Find the length of segment 
The length of segment 
Note that triangles 






which simplifies to 
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A handicap ramp is 

In this case, we are already given the length of the hypotenuse of the right triangle, but the Pythagorean formula still helps us. Plug and play, remembering that 



Thus, the ramp covers 
All ACT Math Resources

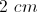





 ,
,  , and
, and  are collinear (they lie along the same line).
are collinear (they lie along the same line).  ,
,  ,
,  ,
, 
















